函数单调性的性质
共479题

· 函数单调性的性质

函数单调性的性质
共479题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

已知函数有两个零点.

26.求a的取值范围；

27.设x1,x2是的两个零点,证明：.

第(1)小题正确答案及相关解析

正确答案

；

解析

试题分析：本题属于导数的综合应用问题，属于拔高题，不容易得分，解析如下：

（Ⅰ）．

（i）设,则,只有一个零点．

（ii）设,则当时,；当时,．所以在上单调递减,在上单调递增．

又,,取满足且,则

故存在两个零点．

（iii）设,由得或．

若,则,故当时,,因此在上单调递增．又当时,,所以不存在两个零点．

若,则,故当时,；当时,．因此在单调递减,在单调递增．又当时,,所以不存在两个零点．综上,的取值范围为．

考查方向

本题考查了利用导数求参数的范围、利用零点证明不等式等知识点。

解题思路

求导，根据导函数的符号来确定，主要要根据导函数的零点来分类讨论；

易错点

第二问对题中所给条件不知如何下手导致失分。

第(2)小题正确答案及相关解析

正确答案

见证明。

解析

试题分析：本题属于导数的综合应用问题，属于拔高题，不容易得分，解析如下：

由已知得：，不难发现，，

故可整理得：

设，则

那么，当时，，单调递减；当时，，单调递增．

设，构造代数式：

设，

则，故单调递增，有．

因此，对于任意的，．

由可知、不可能在的同一个单调区间上，不妨设，则必有

令，则有

而，，在上单调递增，因此：

整理得：．

考查方向

本题考查了利用导数求参数的范围、利用零点证明不等式等知识点。

解题思路

借助第一问的结论来证明．

易错点

第二问对题中所给条件不知如何下手导致失分。

题型：简答题

简答题 · 13 分

设函数，曲线在点处的切线方程为，

23.求，的值；

24.求的单调区间.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ），；

解析

考查方向

导数的应用

解题思路

(1)

易错点

用导数判断函数的单调性时，要本着定义域优先的原则，在对函数划分单调区间时，要注意定义区间内的间断点．

第(2)小题正确答案及相关解析

正确答案

（2）的单调递增区间为.

解析

从而.

综上可知，，，故的单调递增区间为.

考查方向

导数的应用

解题思路

(1)

易错点

用导数判断函数的单调性时，要本着定义域优先的原则，在对函数划分单调区间时，要注意定义区间内的间断点．

题型：单选题

单选题 · 5 分

12.已知函数为的零点,为图像的对称轴,且在单调,则的最大值为

A11

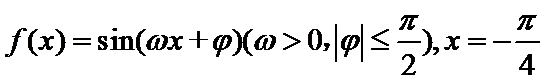
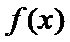
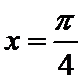
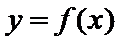
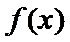
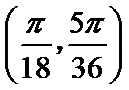
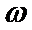
正确答案

解析

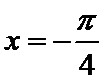
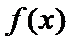
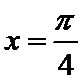
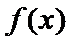
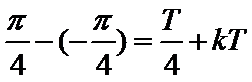
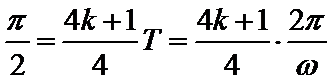
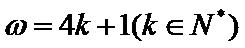
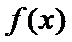
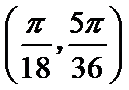
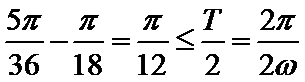
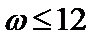
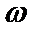
试题分析：因为为的零点，为图像的对称轴，所以，即，所以，又因为在单调，所以，即，由此的最大值为9.故选B.

考查方向

本题主要考查了正弦型函数的图像及性质等知识点，为高考常考题，在近几年的各省高考题出现的频率较高，常与正弦型函数的图像、性质等知识点交汇命题。

解题思路

先根据函数的零点及对称性求出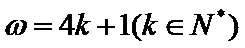，再根据单调性即可求出其最大值.

易错点

正弦函数的性质不熟悉导致出错。

知识点

函数单调性的性质

题型：单选题

单选题 · 5 分

8.已知函数f（x）=（a>0,且a≠1）在R上单调递减，且关于x的方程恰好有两个不相等的实数解，则a的取值范围是（）

A（0，]

B[，]

C[，]{}

D[，）{}

正确答案

解析

由在上递减可知，由方程恰好有两个不相等的实数解，可知，，又∵时，抛物线与直线相切，也符合题意，∴实数的去范围是，故选C.

考查方向

本题主要考查了函数的单调性、图像、函数的零点等知识点，为高考常考题，在近几年的各省高考题出现的频率较高，常与函数的图像、性质等知识点交汇命题。

解题思路

根据函数的单调性先求出，再由程恰好有两个不相等的实数解求出，再检验时是否符合题意。

易错点

忽略时符合题意导致出错。

教师点评

函数性质综合应用

知识点

函数单调性的性质函数零点的判断和求解二次函数的零点问题

题型：单选题

单选题 · 5 分

12. 已知函数在上处处可导，若，则（）．

A 一定小于

B 一定大于

C 可能大于

D可能等于

正确答案

解析

构造函数则

因为所以，即在上递增，

所以，于是，

故选A。

考查方向

本题主要考查构造函数比较两个数大小的方法，导数与函数的单调性等知识，是一道综合性较强的问题。

解题思路

（1）根据题意构造函数。

（2）确定函数的单调性。

（3）利用单调性比较大小。

易错点

（1）不能根据题意构造函数。

（2）求函数导数时，出现错误。

知识点

函数单调性的判断与证明函数单调性的性质导数的运算

继续学习学习下一知识点

下一知识点 : 复合函数的单调性

百度题库 > 高考 > 理科数学 > 函数单调性的性质

扫码查看完整答案与解析