- 函数单调性的性质
- 共479题
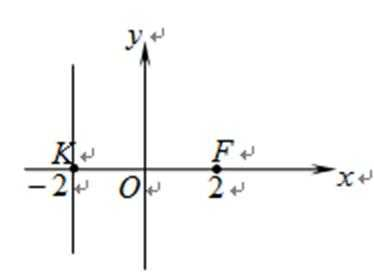
定义域为R的函数




正确答案
解析
当



当


∴当

当

当

所以当




所以不等式等价于





知识点
函数






(1)直接写出不等式
(2)求证:所有的点

(3)求证:点

正确答案
见解析
解析
(1)
(2)∵

∴


第
所以过

同理可得过

所以
直线方程为

同理最低点:

知识点
设数列{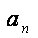
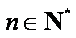
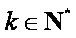
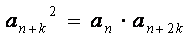
数列{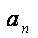
(1)若数列{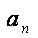
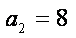
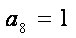
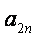
(2)若数列{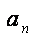
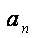
正确答案
见解析
解析
解:(1)由题意,得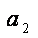
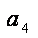
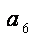
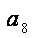
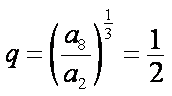
所以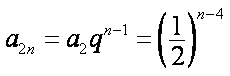
(2)证明:由{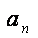
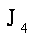
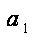
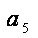
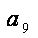
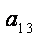
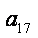
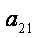
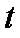
由{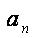
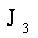
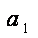
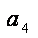
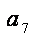
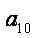
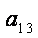
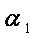
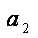
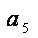
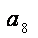
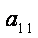
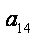
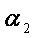
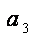
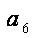
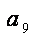
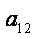
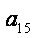
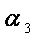
则


所以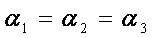
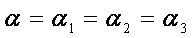
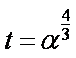
于是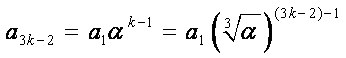
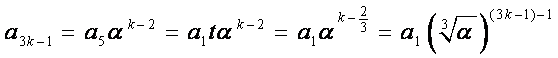
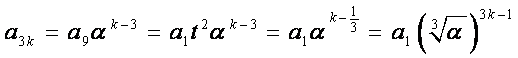
所以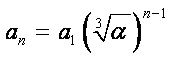
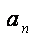
知识点
正确答案
(1)①
(2)


解析
解析:①由


所以
即

②连接

所以
即
(2)①由
得当



此时
当



②
当且仅当



当



知识点
已知函数
(1)设P,Q是函数
(2)求实数


正确答案
见解析
解析
解:(1)由题意,得
所以函数
设



(2)当

当


①当


所以

所以
②当


于是
因为


所以

所以

亦即
(i)当


所以


(ii)当


当



从而

综上所述,实数

知识点
已知动点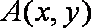
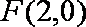
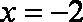
(1)求动点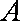
(2)记点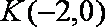

正确答案
(1)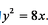
解析
解析:(1)由题意可知,动点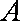
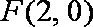
设方程为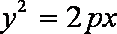

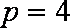
所以动点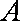
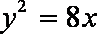
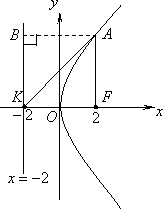
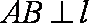
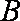
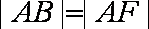
由于
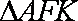
………2分

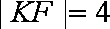
所以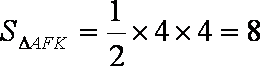
知识点
定义



正确答案
解析
由定义可知,







知识点
已知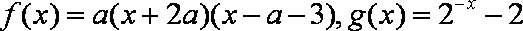
①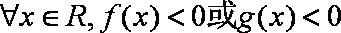
②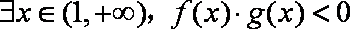
则实数a的取值范围是
正确答案
解析
由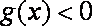
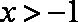
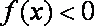
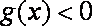
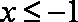
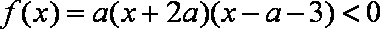
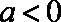
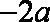
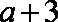
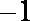
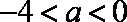
因为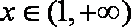
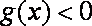
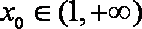
只要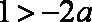
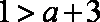
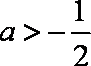
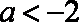

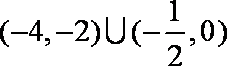
知识点
在区间

为 。
正确答案
解析
函数有零点,则







知识点
已知函数
(1)求函数
(2)求函数

正确答案
见解析
解析
解: (1)因为
故
(2)当
故所求的值域为
知识点
扫码查看完整答案与解析