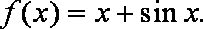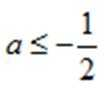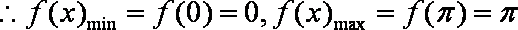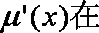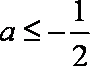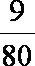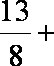- 函数单调性的性质
- 共479题
已知函数
(1)当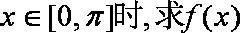
(2)设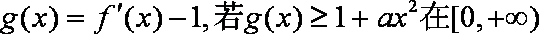
正确答案
(1)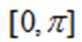
解析
(1) 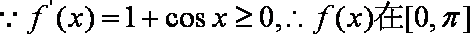
所以函数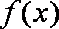
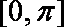
(2)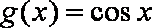
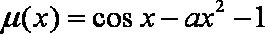
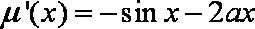
当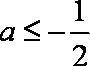
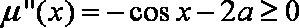
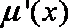
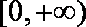
又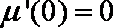
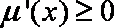
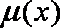
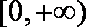
所以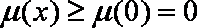
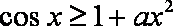
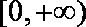
当
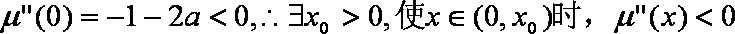
所以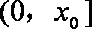
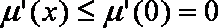
故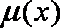
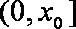
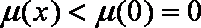
综上,故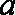
知识点
在平面直角坐标系









正确答案
见解析。
解析



即

直线

所以直线

知识点
设函数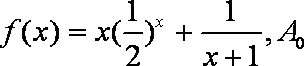
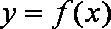
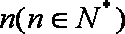
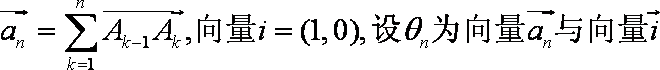

正确答案
解析
由题意知An=(n,f(n)),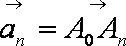
tanθn=
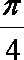
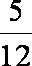
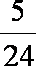
则有 1+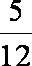
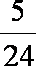
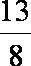

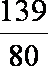
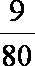
知识点
(1)求证:数列{an,-1)是等比数列;
(2)当n取何值时,bn取最大值,并求出最大值;
(3)若
正确答案
见解析
解析
(1)∵


∴

又



∵
∴


(2)由(1)可知


∴

当n=7时,

当n<7时,

当n>7时,

∴当n=7或n=8时,

(3)由

依题意(*)式对任意
①当t=0时,(*)式显然不成立,因此t=0不合题意,…………9分
②当t<0时,由


而当m是偶数时
③当t>0时,由

∴


设

∵

∴
∴

所以实数

知识点
已知点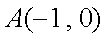
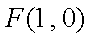
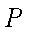
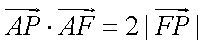
(1)求动点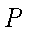
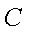
(2)在直线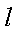
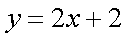
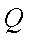
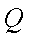
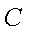
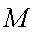
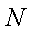
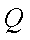
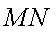
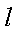
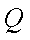
正确答案
见解析。
解析
(1)设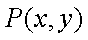
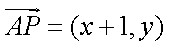
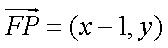
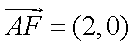
由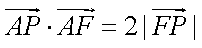
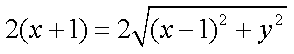
化简得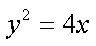
故动点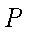
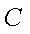
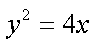
(2)直线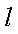
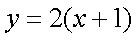
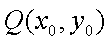
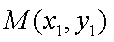
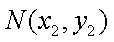
过点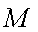
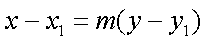
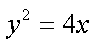
得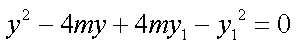
由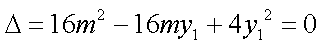
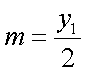
所以过点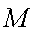
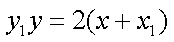
同理过点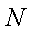
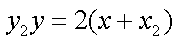
所以直线MN的方程为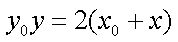
又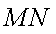
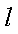
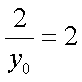
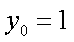
而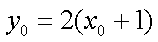
故点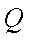
知识点
扫码查看完整答案与解析