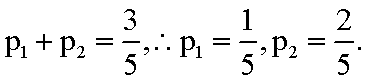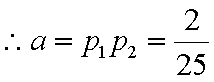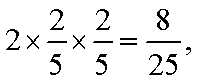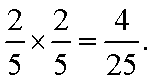- 函数单调性的性质
- 共479题
设函数f(x) =ex(sinx—cosx),若0≤x≤2012π,则函数f(x)的各极大值之和为
正确答案
解析
∵函数f(x)=ex(sinx-cosx),∴f′(x)=(ex)′(sinx-cosx)+ex(sinx-cosx)′=2exsinx,
∵x∈(2kπ,2kπ+π)时,f′(x)>0,x∈(2kπ+π,2kπ+2π)时,f′(x)<0,
∴x∈(2kπ,2kπ+π)时原函数递增,x∈(2kπ+π,2kπ+2π)时,函数f(x)=ex(sinx-cosx)递减,故当x=2kπ+π时,f(x)取极大值,其极大值为f(2kπ+π)=e2kπ+π[sin(2kπ+π)-cos(2kπ+π)]=e2kπ+π×(0-(-1))=e2kπ+π,又0≤x≤2012π,∴函数f(x)的各极大值之和S=eπ+e3π+e5π+…+e2011π=
知识点
某医疗设备每台的销售利润与该设备的无故障使用时间Q(单位:年)有关,若Q≤1,则销售利润为0元;若1<Q≤3,则销售利润为10万元;若Q>3,则销售利润为20万元.已知每台该种设备的无故障使用时间Q≤1,1<Q≤3及Q>3这三种情况发生的概率分别为p1,p2,p3,又知p1,p2是方程25x2-15x+a=0的两个根,且p2=p3.
(1))求a的值;
(2)记两台这种设备的销售利润之和为ξ,求ξ的分布列和期望。
正确答案
见解析
解析
(1)由已知得p1+p2+p3=1,
∵p2=p3,∴p1+2p2=1. ∵p1,p2是方程25x2-15x+a=0的两个根,
∴
(2)ξ的可能取值为0,10,20,30,40.
P(ξ=0)=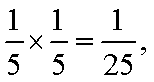
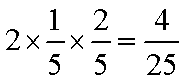
P(ξ=20)=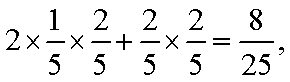
P(ξ=40)=
随机变量ξ的分布列为:

E(ξ)=
知识点
已知点


正确答案
见解析
解析
解:根据椭圆的参数方程, 可设点
则

知识点
如图, 等边三角形






求证: 
正确答案
见解析
解析
证明:∵三角形



所以

同理, 



知识点
已知数列






(1)若数列


(2)若




(3)若









证明:
正确答案
见解析
解析
(1)解:由题意得:



(2)因为 


…… 
由于







由于

根据“生成数列”的定义知,数列

(3)证法一:
证明:设数列





由(2)中结论可知 

所以,

所以
证法二:
因为 
所以 
所以欲证

对于数列

因为 


…… 
由于




相加得

设数列



所以 

同理可证,

所以 
知识点
扫码查看完整答案与解析