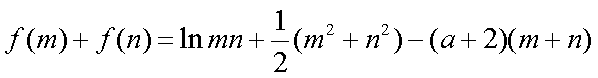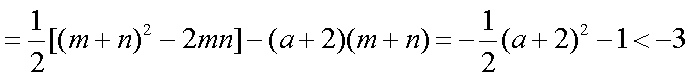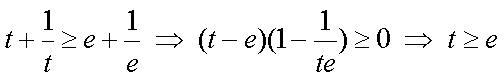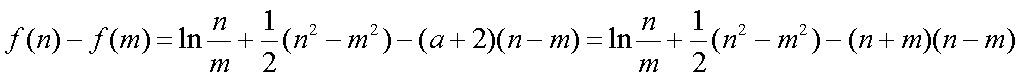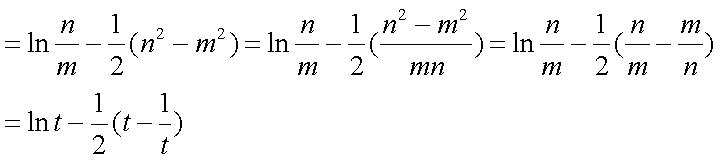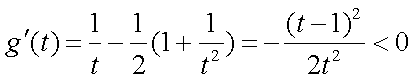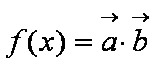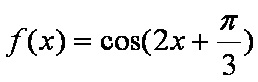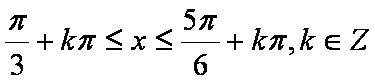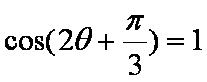- 函数单调性的性质
- 共479题
设
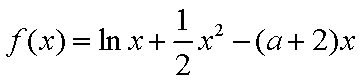
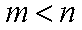
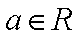
(1) 求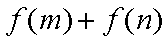
(2) 若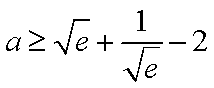
正确答案
见解析
解析
(1)解:函数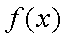
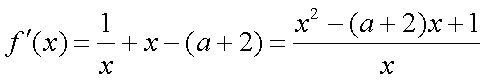
依题意,方程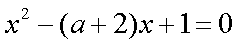
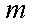
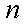
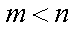
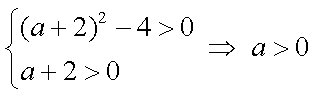
并且 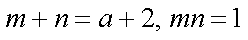
所以,
故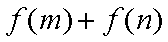
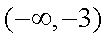
(2)解:当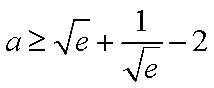
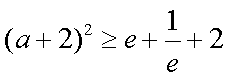
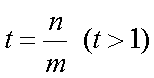
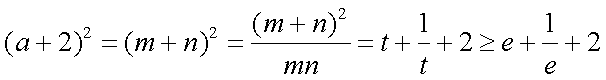
于是有
构造函数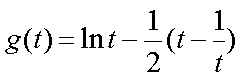
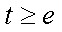

所以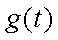
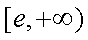
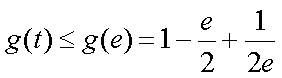
故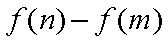
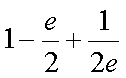
知识点
曲线C的极坐标方程是




正确答案
解析
∵曲线C的极坐标方程是p=2sinθ,两边同时乘以ρ,化为普通方程为 x2+y2=2y,即 x2+(y-1)2=1,表示以(0,1)为圆心,以1为半径的圆,直线l的参数方程是


知识点
若实



正确答案
-1
解析
解析:设f(y)=


当且仅当4cos2(xy)=



知识点
已知向量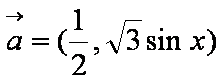
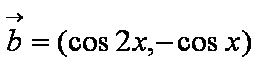
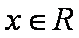
(1)求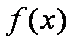
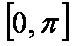
(2)若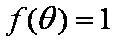
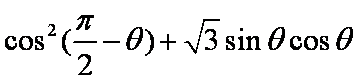
正确答案
见解析
解析
(1)
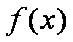
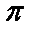
由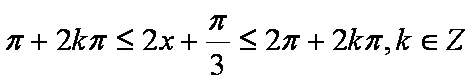
又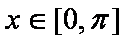
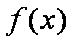
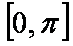
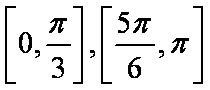
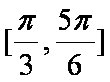
(2)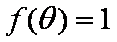
∴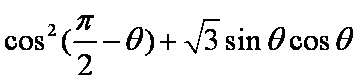
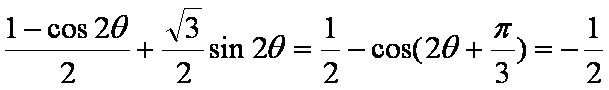
知识点
已知a,b,c为正数,且满足acos2θ+bsin2θ<c,求证:
正确答案
故答案为{1}。
解析
证明:由柯西不等式,得
≤[(


=(acos2θ+bsin2θ)
<
知识点
扫码查看完整答案与解析