- 异面直线的判定
- 共23题
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(1)求证:A1C⊥平面BCDE;
(2)若M是A1D的中点,求CM与平面A1BE所成角的大小;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由
正确答案
见解析
解析




又

又


(2)如图建系



∴
设平面
则

∴
又∵
∴
∴
∴


(3)设线段



则
设平面

则
∴
假设平面

则



∵




知识点
如图,正方体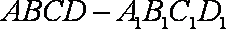
(1)求直线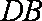
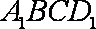
(2)求四棱锥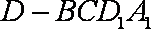
正确答案
(1)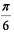
解析
解析:(1)以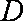
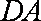
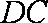
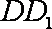
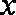
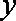
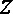
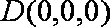
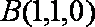
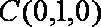
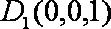
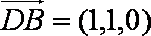
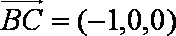

设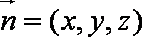
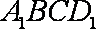
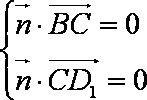
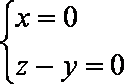
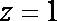
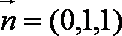
设直线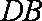
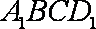
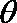
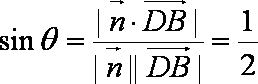
由于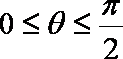
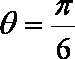
即直线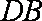
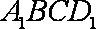
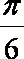
(2)由(1)得
所以点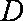
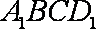
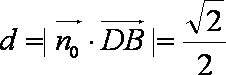
因为四边形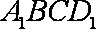
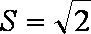
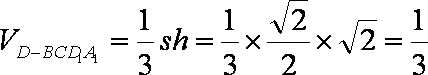
知识点
如右图,在△





正确答案
解析
略
知识点
一个几何体的三视图如图所示,该几何体的表面积是___________。
正确答案
解析
略
知识点
如图,在直三棱柱


(1)求四棱锥
(2)求异面直线AE与A1C所成的角。
正确答案
见解析
解析
(1)四棱锥


∴
(2)取B1C1的中点E1,连A1E1,E1C,
则AE∥A1E1,∴∠E1A1C是异面直线AE与A1C所成的角。…(8分)
由






所以异面直线AE与A1C所成的角为
知识点
扫码查看完整答案与解析