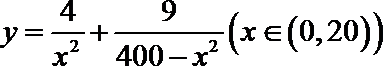- 基本不等式的实际应用
- 共15题
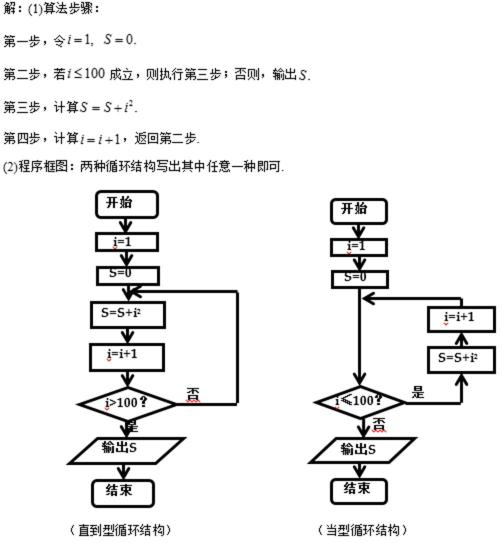
21.两城市A和B相距20km,现计划在两城市外以AB为直径的半圆弧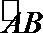
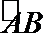
(1)将y表示成x的函数;
(2)判断弧
正确答案
(1)由题意得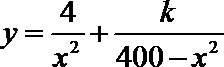
又∵当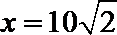
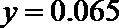
∴
∴
(2)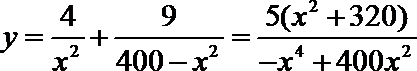
令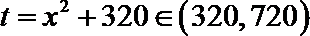
则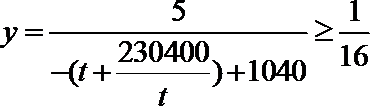
当且仅当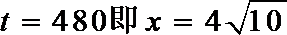
∴弧AB上存在一点,该点到城A的距离为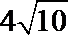
解析
解析已在路上飞奔,马上就到!
知识点
某工厂生产某种产品,每日的成本C(单位:元)与日产里x(单位:吨)满足函数关系式C=3+x,每日的销售额R(单位:元)与日产量x满足函数关系式
(1)求k的值;
(2)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值。
正确答案
见解析。
解析
解:(1)由题意可得:L=
因为x=2时,L=3
所以3=2×2+
所以k=18
(2)当0<x<6时,L=2x+
所以L=2(x﹣8)+


当且仅当2(8﹣x)=
当x≥6时,L=11﹣x≤5
所以当x=5时,L取得最大值6
所以当日产量为5吨时,毎日的利润可以达到最大值6。
知识点
设变量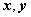
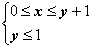
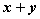
正确答案
解析
略
知识点
设等差数列{



(1)求数列{
(2)设数列{






正确答案
(1)
(2)
解析
(1)解:设等差数列{


因为已知
可得
整理得,
又因为
当
即,
①②联立可得
由于
所以,
(2)解:由(Ⅰ)可得
将

当
当

①-②可得
所以

两式相减得

所以
知识点
已知两条直线










正确答案
解析
在同一坐标系中作出y=m,y=

由




依照题意得


知识点
已知数列



(1)若数列


(2)证明:
正确答案
见解析
解析
(1)解:


证法一:


②-①,得
③-④,得
即

证法二:同证法一,得
令
设
(1)当
(2)假设当

这就是说,当
根据(1)和(2),可知


(2)证明:
知识点
18.某房地产开发公司计划在一楼区内建造一个长方形公园





(1)若设休闲区的长和宽的比




(2)要使公园所占面积最小,休闲区
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 设计一个算法求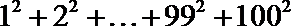
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.甲、乙两公司同时开发同一种新产品,经测算,对于函数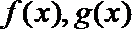
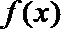
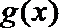
(1)试解释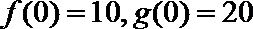
(2)设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.某工厂去年某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n次投入后,每只产品的固定成本为


(1)求k的值,并求出
(2)问从今年算起第几年利润最高?最高利润为多少万元?
正确答案
(1)由
所以
(2)由

当且仅当
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析