- 合情推理与演绎推理
- 共67题
24.设集合



(1)求



(2)猜想
正确答案
(1)



(2)猜想
解析
试题分析:本题属于探究性问题,题目的难度是逐渐由易到难,通过归纳猜想,得出结论,再利用数学归纳法进行证明。
(1)



(2)猜想
下用数学归纳法证明之.
证明:①当
②假设当



则当

而当集合






所以

即
所以当
综上所述,猜想成立.
考查方向
解题思路
本题考查数学归纳法,解题步骤如下:
1、验证当n取第一个值

2、假设当
3、由(1)(2)就可以判定,对于一切n≥
易错点
数学归纳法证明的步骤,尤其第二部归纳递推要过程充分。
知识点
设















正确答案
解析
略
知识点
已知集合







(1)当




(2)(ⅰ)证明:若



(ⅱ)设



说明理由;
(3)记




正确答案
见解析
解析
(1)解:当

得 

由 


(2)(ⅰ)证明:设


因为 

所以 

即 


所以 

所以

(ⅱ)解:设



反例如下:取


则 



因为

所以不存在

(3)解法一:因为 
设






所以
因为 
所以 

所以 
因为

又 
所以

即 
对于 





综上,

解法二:首先证明如下引理:设

证明:因为 

所以 
即 
所以

上式等号成立的条件为


对于 





综上,

知识点
设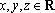
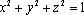


正确答案
解析
略
知识点
若存在正实数




① 



其中“在
正确答案
②③
解析
略
知识点
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”,类似的,我们在平面向量集





①若
②若
③若

④对于任意向量
其中真命题的序号为
正确答案
解析
略
知识点
已知

整数,且



正确答案
41
解析
略
知识点
对于两个图形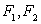
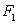
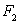
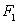
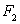
①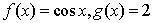
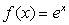
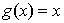
③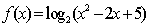
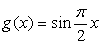
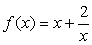
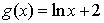
⑤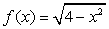
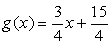
正确答案
②④
解析
略
知识点
对于集合


正确答案
解析
略
知识点
14.我们知道,把所有的正整数按照不同的方式排列,就会出现很多不同的意义。现在把所有正整数按从小到大的顺序排成如图所示的数表,其中第






正确答案
1004
解析
最后一个数是首项为1,等比为2的前n项和,n+1表示行数,当n=10时,即第11行的最后一个数为2047,第11行共有
考查方向
解题思路
最后一个数是首项为1,等比为2的前n项和,n+1表示行数,当n=10时,即第11行的最后一个数为2047,第11行共有
易错点
找不到规律;推理出错,计算错误都是导致出错的原因。
知识点
扫码查看完整答案与解析