合情推理与演绎推理
共67题

合情推理与演绎推理
共67题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 10 分

17．如图（1），在三角形中，，若，则；若类比该命题，如图（2），三棱锥中，面，若点在三角形所在平面内的射影为，则有什么结论？命题是否是真命题．

正确答案

命题是：三棱锥中，面

若点在三角形所在平面内的射影为

有是一个真命题

证明如下：

在图（2）中，连结，并延长交于

连结，则有

因为面，，所以

又，所以

于是

解析

解析已在路上飞奔，马上就到！

知识点

类比推理

题型：填空题

填空题 · 4 分

14．对于任意一个非零实数，它的倒数的倒数是它的本身。也就是说，连续施行两次倒数变换后又回到施行变换前的对象，我们把这样的变换称为回归变换。在中学数学范围内写出这样的变换（写对一个变换给2分，最多得4分）（）

正确答案

相反数的相反数是它本身，集合A的补集的补集是它本身，一个复数的共轭的共轭是它本身，等等.

解析

解析已在路上飞奔，马上就到！

知识点

类比推理

题型：填空题

填空题 · 5 分

7．在共有2013项的等差数列{an}中，有等式(a1＋a3＋…＋a2013)－(a2＋a4＋…＋a2012)＝a1007成立；类比上述性质，在共有2011项的等比数列{bn}中，相应的有等式（）成立。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用等比数列的性质及应用类比推理

题型：填空题

填空题 · 5 分

14.求“方程5x+12x=13x的解”有如下解题思路:设f（x）=（）x+（）x,则f（x）在R上单调递减,且f（2）=1,所以原方程有唯一解x=2.类比上述解题思路,方程x3+x=+的解为________.

正确答案

x=-1或x=1

解析

类比上述解题思路,设f(x)=x3+x,由于f'(x)=3x2+1≥0,则f(x)在R上单调递增,∵x3+x=+,∴x=,解得x=-1或x=1.

知识点

类比推理

题型：简答题

简答题 · 14 分

29．在平面直角坐标系中，对于点、直线，我们称为点到直线的方向距离。

（1）设椭圆上的任意一点到直线的方向距离分别为，求的取值范围。

（2）设点、到直线：的方向距离分别为、，试问是否存在实数，对任意的都有成立？若存在，求出的值；不存在，说明理由。

（3）已知直线：和椭圆：（），设椭圆的两个焦点到直线的方向距离分别为、满足，且直线与轴的交点为、与轴的交点为，试比较的长与的大小。

正确答案

（1）；

（2）；

（3）

（1）由点在椭圆上，所以

由题意、，于是

又得，即

（也可以先求出，再利用基本不等式易得）

（2）假设存在实数，满足题设，

由题意，

于是

对任意的都成立

只要即可，所以

故存在实数，，对任意的都有成立。

（学生通过联想，判断直线是椭圆的切线，又证明从而得到也给分）

（3）设的坐标分别为、，于是

、于是

又，即

所以

综上

解析

试题分析：本题属于圆锥曲线中的基本问题，题目的难度是逐渐由易到难，

（1）直接按照步骤来求

（2）要注意对参数的讨论．

考查方向

本题考查了直线与椭圆的位置关系，属于高考中的高频考点

解题思路

本题考查圆锥曲线与直线的位置关系，解题步骤如下：

1、利用新定义求解。

2、联立直线与椭圆方程求解。

易错点

第二问中表示直线斜率时容易出错。

知识点

类比推理进行简单的合情推理分析法的思考过程、特点及应用综合法的思考过程、特点及应用

题型：填空题

填空题 · 4 分

设,以间的整数为分子，以为分母组成分数集合，其所有元素和为；以间的整数为分子，以为分母组成不属于集合的分数集合，其所有元素和为；……，依次类推以间的整数为分子，以为分母组成不属于的分数集合，其所有元素和为；则=________.

正确答案

解析

略

知识点

元素与集合关系的判断等差数列的前n项和及其最值进行简单的合情推理

题型：简答题

简答题 · 13 分

已知集合，对于，，定义；

；与之间的距离为。

（1）当时，设，，若，求；

（2）（ⅰ）证明：若，且，使，则；

（ⅱ）设，且，是否一定，使？

说明理由；

（3）记，若，，且，求的最大值。

正确答案

见解析

解析

（1）解：当时，由，

得，即。

由，得，或。 ………………3分

（2）（ⅰ）证明：设，，。

因为，使，

所以，使得，

即，使得，其中。

所以与同为非负数或同为负数。 ………………5分

所以

。 ………………6分

（ⅱ）解：设，且，此时不一定，使得

。 ………………7分

反例如下：取，，，

则，，，显然。

因为，，

所以不存在，使得。 ………………8分

（3）解法一：因为，

设中有项为非负数，项为负数，不妨设时；时，。

所以

因为，

所以，整理得。

所以。……………10分

因为

；

又，

所以

。

即。 ……………12分

对于，，有，，且，

。

综上，的最大值为。 ……………13分

解法二：首先证明如下引理：设，则有。

证明：因为，，

所以，

即。

所以

。 ……………11分

上式等号成立的条件为，或，所以。 ……………12分

对于，，有，，且，

。

综上，的最大值为。 ……………13分

知识点

平行向量与共线向量分组转化法求和进行简单的合情推理绝对值三角不等式

题型：填空题

填空题 · 5 分

设，且满足：，，则_________.

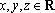
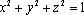
正确答案

解析

略

知识点

进行简单的合情推理一般形式的柯西不等式

题型：填空题

填空题 · 5 分

若存在正实数，对于任意，都有，则称函数在上是有界函数，下列函数

① ；②；③；④，

其中“在上是有界函数”的序号为__________。

正确答案

②③

解析

略

知识点

函数的值域进行简单的合情推理

题型：填空题

填空题 · 5 分

在实数集R中，我们定义的大小关系“＞”为全体实数排了一个“序”，类似的，我们在平面向量集上也可以定义一个称为“序”的关系，记为“”.定义如下：对于任意两个向量当且仅当“”或“”.按上述定义的关系“”，给出如下四个命题：

①若；

②若；

③若，则对于任意；

④对于任意向量.

其中真命题的序号为

正确答案

解析

略

知识点

命题的真假判断与应用平面向量数量积的运算进行简单的合情推理

继续学习学习下一知识点

下一知识点 : 直接证明、间接证明、数学归纳法

百度题库 > 高考 > 理科数学 > 合情推理与演绎推理

扫码查看完整答案与解析