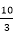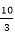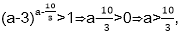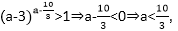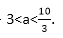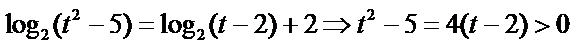- 指数幂的运算
- 共43题
1
题型：
单选题
|
6.已知定义在R上的奇函数f（x）满足f（x+4）+f（x）=0,且在[2,4]上是增函数,又a=lg 8,b=log23,c>0且104-c<8,则有（ ）.
正确答案
B
解析
∵f(x)是奇函数,∴f(x+4)=-f(x)=f(-x),∴函数f(x)关于x=2对称.∵f(x)在[2,4]上是增函数,∴f(x)在[0,2]上是减函数.由c>0且104-c<8,得0<4-c<lg 8.又0<lg 8<1,1<log23<2,∴0<a<b,∴f(a)>f(b),f(c)>f(a),即f(c)>f(a)>f(b).
知识点
指数幂的运算
1
题型：
单选题
|
2.若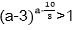
Aa>4
Ba>-4
C3<a<
Da>4或3<a<
正确答案
D
解析
当a-3>1,即a>4时,
由
结合a>4,得a>4.
当0<a-3<1,
即3<a<4时,
由
结合3<a<4,
得
知识点
指数幂的运算指数函数单调性的应用其它不等式的解法
1
题型：填空题
|
2．方程
正确答案
解析
∵
∴方程
考查方向
本题主要考查了对数方程的解法，考查学生计算能力，属于容易题．
易错点
在对数方程的求解中，将对数式转化成指数式的过程中，特别要注意对数式中的底数、真数、对数与指数式中的底数、幂、指数的对应关系．
知识点
指数幂的运算对数的运算性质
1
题型：填空题
|
7．方程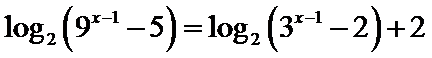
正确答案
解析
设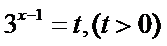
知识点
指数幂的运算对数的运算性质
1
题型：
单选题
|
2.设函数
正确答案
B
解析
考查方向
本题主要考查分段函数函数值的求法以及指数、对数的性质和运算法则。重在考查学生对于指数和对数的运算化简能力。
解题思路
1、先求
2、
易错点
1.不会将
2.忘记公式
知识点
函数的值指数幂的运算对数的运算性质
下一知识点 : 指数函数的定义、解析式、定义域和值域
扫码查看完整答案与解析