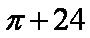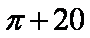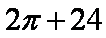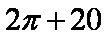- 组合几何体的面积、体积问题
- 共98题
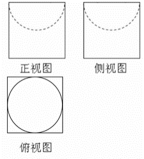
某几何体的主视图与俯视图如图所示，左视图与主视图相同，且图中的四边形都是边长为2的正方形，两条虚线互相垂直，则该几何体的体积是（）
A
B
C6
D4
正确答案
解析
略
知识点
如图，一个空间几何体的正视图、侧视图是周长为4一个内角为60°的菱形，俯视图是圆及其圆心，那么这个几何体的表面积为 。
正确答案
π
解析
解：∵几何体的正视图、侧视图是周长为4一个内角为60°的菱形
∴几何体是由两个底面直径为1，母线长为1的圆锥组合而成，
∴S=2×
故答案为：π
知识点
一个几何体的三视图如图所示，则该几何体的表面积为______________。
正确答案
38
解析
由三视图可知该几何体为一个长方体在中间挖去了一个等高的圆柱，其中长方体的长、宽、高分别为4、3、1，圆柱的底面直径为2，所以该几何体的表面积为长方体的表面积加圆柱的侧面积再减去圆柱的底面积，即为
知识点
如图是一个无盖器皿的三视图，正视图、侧视图和俯视图中的正方形
边长为2，正视图、侧视图中的虚线都是半圆，则该器皿的表面积是
A
B
C
D
正确答案
解析
略
知识点
一个几何体的三视图如图所示，则这个几何体的体积为
正确答案
解析
由三视图可知该几何体左边为半个圆锥，右边为底面是正方形的四棱锥，所以其体积为
知识点
一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的全面积为
A
B
C
D
正确答案
解析
几何体为底面半径为
知识点
某个
A
B
C
D
正确答案
解析
略
知识点
己知某几何体的三视图如图所示，根据图中标出的尺寸（单位cm），可得这个几何体的体积是 cm3。
正确答案
解析
由三视图可知：该几何体是一个由上下两部分组成的几何体，其中上面是一个上下底面半径分别为2，1，高为1的圆台；
下面是一个半径分别为1，母线长为3的圆柱。
因此该几何体的体积V=
故答案为
知识点
某几何体的三视图如图所示，则这个几何体的体积为
A4
B
C
D8
正确答案
解析
三视图可知，该几何体可分为一个三棱锥和一个四棱锥，
则
知识点
下图是一个几何体的三视图，根据图中数据，可得该几何体的体积是______________。
正确答案
解析
由三视图可知几何体为组合体，上方是一个卧式直三棱柱，三棱柱的底面是其中一边长为
知识点
扫码查看完整答案与解析