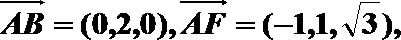- 组合几何体的面积、体积问题
- 共98题
5.如图为某几何体的三视图,则该几何体的表面积为( )
正确答案
解析
由还原后的几何体为半个圆柱和一个正方体组成,且圆柱底面半径为1,高是2,正方体的棱长为2,得S=
考查方向
本题主要考查三视图
解题思路
1、还原几何体;
2、利用表面积公式求解,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在还原几何体时发生错误。
知识点
7.如图,网格纸是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为( )
正确答案
解析
由图可知,此多面体是一个以4为高,以长和宽分别是6、2的矩形为底的四棱锥。则V=sh/3=16。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查三视图
解题思路
1、还原几何体;
2、求出体积,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在还原几何体时发生错误。
知识点
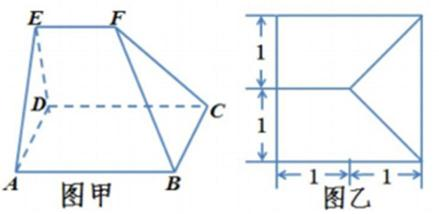
16.多面体ABCDEF(如图甲)的俯视图如图乙,己知面ADE为正三角形.
(1)求多面体ABCDEF的体积;
(2)求二面角A-BF-C的余弦值.
正确答案
(1)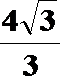
(2)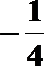
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)分别取AB、CD的中点M、N,连接EM、EN、MN,多面体体积转化为棱柱AED-MFN的体积V1与四棱锥F-MBCN的体积V2之和。
由三视图可知,AD=2,AM=DN=1,面ADE为正三角形且垂直于底面ABCD,知F点到底面的距离为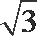
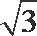
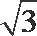
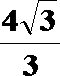
(2) 取MN的中点O,BC的中点P,以OM为x轴,OP为y轴,OF为z轴建立坐标系,
易知A(1,-1,0),B(1,1,0),F(0,0, 
设面ABF的法向量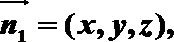
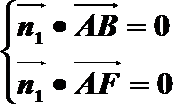
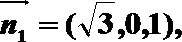
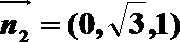

考查方向
本题考查了立体几何中的体积和二面角的问题.属于高考中的高频考点。
解题思路
本题考查立体几何中的体积和二面角的问题,解题步骤如下:
(1)做辅助线,拆分多面体。
(2)建立空间直角坐标系。
(3)利用夹角的余弦公式求解。
易错点
(1)第一问中的多面体的拆分。
(2)第二问中二面角的求解时要建立适当的空间直角坐标系。
知识点
8.一个长方体被一个平面截去一部分后所剩几何体的三视图如右图所示 (单位:cm),则该几何体的体积为( )
正确答案
解析
原几何体的体积为
考查方向
本题主要考查解利用三视图求几何体的体积
解题思路
通过三视图可知,几何体的体积是利用正方体体积减去三棱锥的体积
易错点
不会利用三视图复原直观图
知识点
5.一个几何体的三视图如图所示,那么这个几何体的表面积是( )
正确答案
解析
由三视图,可知该几何体的直观图如图所示,面








考查方向
解题思路
1.根据几何体的三视图,画出该几何体的直观图;
2.分别判定几何体各面的形状求其面积;
3.求和,即得该几何体的表面积。
易错点
本题易在求侧面

知识点
扫码查看完整答案与解析