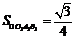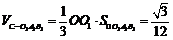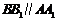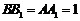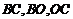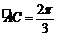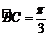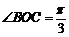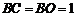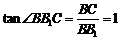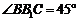- 组合几何体的面积、体积问题
- 共98题
10．已知一个几何体的三视图如右图所示，则该几何体的体积为（ ）
A
B
C
D
正确答案
知识点
6.某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）
A
B
C
D1
正确答案
知识点
18.（本小题满分12分）
如图，在四棱锥P-ABCD中，AD∥BC，
（I）在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；
（II）若二面角P-CD-A的大小为45°，求直线PA与平面PCE所成角的正弦值.
正确答案
知识点
10. 在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球，若AB
A4π
B
C6π
D
正确答案
知识点
正确答案
知识点
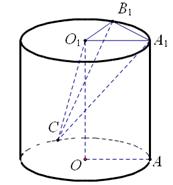
19.（本题满分12分）将边长为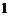
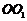
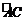
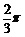
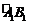
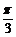
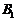
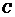
(1) 求三棱锥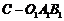
(2) 求异面直线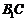
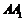
正确答案
(1) 连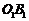
∴
∴
∴
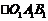
(2) 设点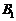
∴
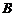
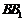
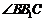
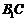
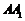
连
∴
∴
∴
∴
∴
∴
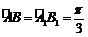
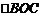
∴直线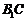
知识点
5.一个几何体的三视图如图，则该几何体的体积为（ ）
A
B
C
D
正确答案
解析
由已知的三视图可得：该几何体是一个以俯视图为底面的半圆锥，其底面面积S=
考查方向
解题思路
由已知的三视图可得：该几何体是一个以俯视图为底面的半圆锥，代入锥体体积公式，可得答案
易错点
本题易在得不出几何体为半圆锥，而且看不清数量关系
知识点
6.一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则
截去部分体积与剩余部分体积的与剩余部分体积的比值为( )
A
B
C
D
正确答案
知识点
7．一个几何体的三视图如图所示，其中正视图与侧视图都是斜边长为2的直角三角形，俯视图是半径为1的四分之一圆周和两条半径，则这个几何体的体积为（ ）
A
B
C
D
正确答案
解析
通过观察判断该几何体是一个圆锥的四分之一 高是
考查方向
解题思路
通过三视图的观察判断形状。
易错点
图形观察失误。
知识点
5. 一个几何体的三视图如图所示，那么这个几何体的表面积是（ ）
A
B
C
D
正确答案
解析
由三视图可知其对应的几何体由左侧长、宽、高分别为１，２，２的长方体与右侧一侧面水平放置的三棱柱，其底面为直角边分别为１，２的直角三角形，高为２的直三棱柱
组合而成，由两个边长为２的正方形，１个长、宽分别为２，１的长方形，１个长、宽分别为２，
其表面积为：
考查方向
解题思路
首先，构建出三视图所对应的空间几何体后，然后依据其结构特征分别计算各面积之和即可。
易错点
本题易在由三视图想象其对应几何体时出错，另外在计算其表面积时组合体的结合部分面积易重复计算而出错。
知识点
扫码查看完整答案与解析