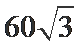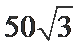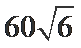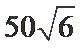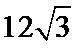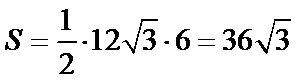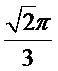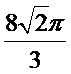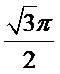- 组合几何体的面积、体积问题
- 共98题
10.球
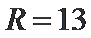

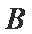
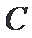
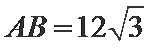
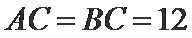
正确答案
解析
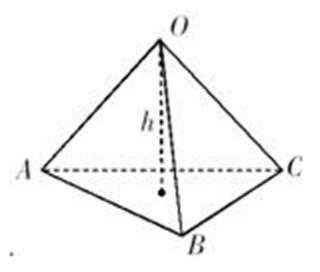
球心O与A,B,C,三点构成的四面体如下图所示,所以底面ABC的面积为底乘以高,底为AB=
高为6,因为球的半径为13,所以圆心到面ABC的距离为12,所以底面面积为
所以体积为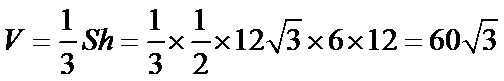
考查方向
解题思路
先根据题意作出四面体大致图形,然后利用体积公式求解
易错点
空间感不强;计算错误
知识点
利用一个球体毛坯切削后得到一个四棱锥P—ABCD,其中底面四边形ABCD是边长为1的正方形,PA=1,且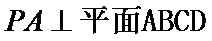
正确答案
解析
由题设知,当所求的球恰为四棱锥的外接球时,球体毛坯体积达到最小值,而此外接球可以与棱长为1的正方体的外接球相同,即
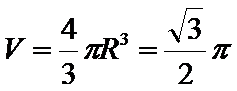
考查方向
解题思路
由题设当所求的球恰为四棱锥的外接球时,球体毛坯体积达到最小值,而此外接球可以转化棱长为1的正方体的外接球,进而求出半径,再求出球的体积。
易错点
1、无法把问题转化为求四棱锥的外接球进而思路受阻;
2、不会分析如何求外接球的半径。
知识点
如图,菱形




22.求证:

23.若

正确答案
见解析
解析
图,过点




















考查方向
解题思路
解题步骤如下:由平面




易错点
本题易在证明线面垂直、平行或求锥体的体积时发生错误 。
正确答案
几何体
解析
连接


























考查方向
解题思路
解题步骤如下:由于该几何体比较复杂,需要分成2个几何体来求解,根据题目给出的条件,求出每个几何体的底面积和对应的高,即可得到几何体的体积。
易错点
本题易在证明线面垂直、平行或求锥体的体积时发生错误 。
5.《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺.问积几何?答曰:二千一百一十二尺.术曰:周



正确答案
解析
依题意,

考查方向
解题思路
依题意,直接列出等式
易错点
不理解题中“圆堡瑽(圆柱体)的体积为:V=
知识点
棱长为1的正方体





21.当


22.当平面



正确答案
(Ⅰ)略;
解析
(Ⅰ)连接


正方体









考查方向
线面、面面垂直的判定与性质,棱柱、棱锥体积的求法.
解题思路
证



易错点
通过证线面垂直得线线垂直;判断
正确答案

解析
当

取






















设



考查方向
解题思路
证



易错点
通过证线面垂直得线线垂直;判断
扫码查看完整答案与解析