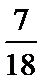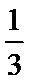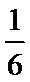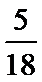- 随机事件的频率与概率
- 共73题
7.2015年高中生技能大赛中三所学校分别有3名、2名、1名学生获奖,
这6名学生要排成一排合影,则同校学生排在一起的概率是 ( )
正确答案
解析
由已知把第一个及第二个学校的学生看做整体得同校学生排在一起共


考查方向
解题思路
1.先求出把第一个及第二个学校的学生看做整体得同校学生排在一起共

易错点
不会相邻问题如何处理;
知识点
2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为



18.求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
19.试求袁先生2016年上半年同时投资甲、乙两只股票的总收益的分布列和数学期望.
正确答案
(1)
解析
(Ⅰ)袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率为
考查方向
解题思路
直接根据题意求即可;
易错点
1.对于题中给出的信息处理出错;2.对于随机变量取值对应的概率出错。
正确答案
((2)
解析
(Ⅱ)用

所以,

考查方向
解题思路
先设出随机变量后写出其取值,然后求其取各个值的概率列分布列带入期望公式即可。
易错点
1.对于题中给出的信息处理出错;2.对于随机变量取值对应的概率出错。
某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
18.求
19.求在未来连续3天里,有连续2天的日销售量都高于100个且另1天的日销售量不高于50个的概率;
正确答案



解析
解:由频率分布直方图,得:



考查方向
解题思路
本题主要考查了统计、独立事件的概率及二项分布的应用,解题步骤如下:由频率算出频率/组距的值再作出对应的图。
易错点
审题不清和考虑不全面导致出错。
正确答案
0.108
∴EX=3×0.6=1.8
解析
解:设A1表示事件“日销售量高于100个”,A2表示事件“日销售量不高于50个”,B表示事件“在未来连续3天里有连续2天日销售量高于10
故所求概率:P(B)=0.6×0.6×0.15×2=0.108.
20.用X表示在未来3天里日销售量高于100个的天数,求随机变量X的分布列和数学期望.
解:依题意,X的可能取值为0,1,2,3,且X~B(3,0.6).
P(X=0)=
P(X=2)=
∴X的分布列为
∴EX=3×0.6=1.8.
考查方向
解题思路
本题主要考查了统计、独立事件的概率及二项分布的应用,解题步骤如下:
根据题设求出相应概率。
本题主要考查了统计、独立事件的概率及二项分布的应用,解题步骤如下:分析
易错点
审题不清和考虑不全面导致出错。
审题不清和考虑不全面导致出错。
为向国际化大都市目标迈进,沈阳市今年新建三大类重点工程,它们分别是30项基础设施类工程,20项民生

19.求这3人选择的项目所属类别互异的概率;
20.将此3人中选择的项目属于基础设施类工程或产业建设类工程的人数记为


正确答案
解析
记第

由题意知
则
3人选择的项目所属类别互异的概率:
考查方向
解题思路
第一问属于古典概型,直接用排列组合求出个数;
易错点
容易在排列组合问题计算时出现错误。
正确答案
解析
任一名工人选择的项目属于基础设施类或产业建设类工程的概率:
由

其数学期望为
考查方向
解题思路
第二问中属于二项分布,各个事件之间是相互独立的,直接用公式求。
易错点
容易在排列组合问题计算时出现错误。
6. 从3名男同学,2名女同学中任选2人参加体能测试,则选到的2名同学中至少有一名女同学的概率是 .
正确答案
解析
从3名男同学,2名女同学中任选2人参加体能测试的选法有


考查方向
解题思路
1.先利用排列组合求出从3名男同学,2名女同学中任选2人参加体能测试的选法有多少种;
2.利用间接法求出其中选到的2名同学中至少有一名女同学的选法有多少种;3.利用古典概型的概率公式求解。
易错点
1.在求选到的2名同学中至少有一名女同学时只考虑女同学由几个,没有考虑到男同学,导致结果出错;
2.不会间接考虑问题。
知识点
8.若以连续掷两次骰子分别得到的点数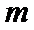
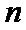
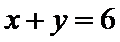
正确答案
解析
以连续掷两次骰子分别得到的点数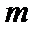
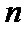

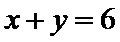
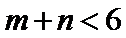
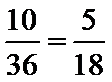
考查方向
解题思路
1.先求出以连续掷两次骰子分别得到的点数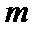
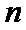
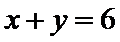
易错点
1.不会计算连续掷两次骰子共有多少种情况;2.不会求点P在直线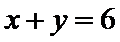
知识点
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得
19.根据以上资料完成下面的2×2列联表,若据此数据算得
20.以此“满意”的频率作为概率,求在3人中恰有2人满意的概率;
21.从以上男性用户中抽取2人,女性用户中抽取1人,其中满意的人数为

正确答案
(1)在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关;
解析
:(Ⅰ)
∵
∴在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关。
考查方向
解题思路
先将题中给出的茎叶图处理成列联表,然后带入求得
易错点
将茎叶图处理成列联表数据出错,
在求
正确答案
(2)
解析
(Ⅱ)由频率估计“满意”的概率为
∴在3人中恰有2人满意的概率为

考查方向
解题思路
先求出“满意”的概率,然后利用n次独立重复试验的概率求法求出概率;
易错点
求概率时忘记乘以
正确答案
(3)

数学期望
解析
(Ⅲ)





数学期望
考查方向
解题思路
先求出随机变量的取值和取各个值的概率后利用公式求出其期望。
易错点
不会求随机变量取各个值的概率。
9.已知一次函数





正确答案
解析
f(0)=-1;f(1)=a-1, 使得



考查方向
解题思路
由于是直线型函数,求两个端点值,f(1)=a-1<0,解得 a
易错点
对于恒成立问题理解错,数形结合应用。
知识点
以下茎叶图记录了甲、乙两组各四名同学的植树棵树,乙组记录中有一个数据模糊,无法确认,在图中以X表示。
19.如果X=8,求乙组同学植树棵树的平均数和方差。
20.如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y的分布列和数学期望。
正确答案
解析
当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10。………2
所以平均数为
方差为
考查方向
解题思路
按题意直接求平均,按公式直接求方差
易错点
第(2)问随机变量找不准,对应有概率计算不准确。
正确答案
随机变量Y的分布列为:
数学期望19
解析
当X=9时,由茎叶图可知,甲组同学的植树棵树是:9,9,11,11;
乙组同学的植树棵数是:9,8,9,10。
分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能的结果,
这两名同学植树总棵数Y的可能取值为17,18,19,20,21。
事件“Y=17”等价于“甲组选出的同学植树9棵,乙组选出的同学植树8棵”,
所以该事件有2种可能的结果,
因此P(Y=17)=
同理可得P(Y=18)=



所以,随机变量Y的分布列为:
EY=17×




考查方向
解题思路
统计事件总为4×4=16,总棵数Y的可能取值为17,18,19,20,21。算出概率,列分布列,直接求数学期望
易错点
第(2)问随机变量找不准,对应有概率计算不准确。
周立波是海派清口创始人和《壹周·立波秀》节目的主持人,他的点评视角独特,语言幽默犀利,给观众留下了深刻的印象.某机构为了了解观众对《壹周·立波秀》节目的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
19.从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
20,根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关.(精确到0.001)
21.从19题中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱《壹周·立波秀》节目的概率.
正确答案
喜爱的观众有4名;不喜爱的观众有2名.
解析
抽样比为

考查方向
解题思路
直接计算抽样比,即可算出喜爱与不喜爱的人数;
易错点
对“独立性检验的思想”不理解易出错
正确答案
不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
解析
假设:观众性别与喜爱无关,由已知数据可求得,
∴ 不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
考查方向
解题思路
直接代入公式计算
易错点
对“独立性检验的思想”不理解易出错
正确答案
0.4
解析
记喜爱的4名男性观众为a,b,c,d,不喜爱的2名男性观众为1
其中选到的两名观众都喜爱的事件有6个,
故其概率为
考查方向
解题思路
直接列出总事件及发生事件的情况,直接求比。
易错点
对“独立性检验的思想”不理解易出错
扫码查看完整答案与解析