等比数列的判断与证明_章节学习

1

题型：简答题

|

简答题 · 16 分

22.给定数列，记该数列前项中的最大项为，即；该数列后项中的最小项为，即；．

（1）对于数列：3,4,7,1，求出相应的；

（2）若是数列的前项和，且对任意有其中为实数，且．

①设，证明数列是等比数列；

②若数列对应的满足对任意的正整数恒成立，求实数的取值范围．

正确答案

（1）；

（2）①证明略；②．

解析

（1）当=1时，A1=3，B1=1，从而可求得，

同理可得

（2）①当时，所以

当时，

两式相减得所以

又

所以，数列是以为首项、为公比的等比数列．

②由①知：；

又，

由于

所以由推得

所以对任意的正整数恒成立．

因为所以

由，得，

但且，所以解得，所以

考查方向

本题考查数列的综合应用，突出考查考查推理论证与抽象思维的能力，是难题．数列的综合应用在近几年各省市的高考试卷中频频出现，是高考的热点问题，往往以等差数列、等比数列为载体，涉及递推公式、通项公式、前项和，结合数列单调性、数列恒成立等知识交汇命题．

解题思路

题（1），当=1时，A1=3，B1=1，从而可求得，同理可求得的值；

题（2）①，利用等比数列的定义证明是等比数列，对含有的表达式，先利用（）求得与递推关系，将代入递推关系化简求得，同时验证的初始值，从而证明是等比数列；

题（2）②，由①得到的通项公式，根据求得，从而得到关于不等式，解得的取值范围．

易错点

对含有的表达式，往往利用求通项时容易忽视的要求，同时要验证的初始值；对新定义、的不理解；恒成立问题的恰当转化．

知识点

等比数列的判断与证明数列与不等式的综合

1

题型：简答题

|

简答题 · 12 分

18.设数列{an}的前n项和为Sn，己知a1=l，nan+1=(n+2)Sn，n∈N*.求证：是等比数列；设Tn= S1+S2+--+Sn，求证：(n+l) Tn<nSn+1．

正确答案

（1）；

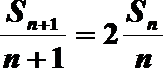
（2）略．

解析

本题属于数列中的基本问题，题目的难度是逐渐由易到难．

（1）由已知得。所以是以1为首项，2为公比的等比数列。

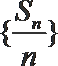
（2）由上知。

……①

……②

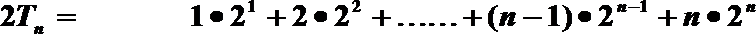
①-②得：。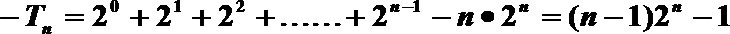

即(n+l) Tn<nSn+1．

考查方向

本题考查了数列的问题．属于高考中的高频考点。

易错点

错位相减法求和时相减的结果项数易错。

知识点

等比数列的判断与证明数列与不等式的综合

1

题型：单选题

|

单选题 · 5 分

5．已知数列是等比数列，是1和3的等差中项，则=

A

B

C

D

正确答案

D

解析

通过观察，可以看到，b2,b16和b9之间的关系，可以得到=b92, ，又根据等差中项的性质，可以得到b9=(1+3)÷2=2,所以=22=4

考查方向

等比数列的定义及性质，等差中项的性质

解题思路

利用等差中项求b9,进而求解答案

易错点

发现不到b2b16和b9之间的关系。

知识点

等比数列的判断与证明

1

题型：单选题

|

单选题 · 5 分

12.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”．

1 2 3 4 5 … 2013 2014 2015 2016

3 5 7 9 ………… 4027 4029 4031

8 12 16 ………………… 8056 8060

20 28 ………………………… 16116

…………………………………………

该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数为________________

A

B

C

D

正确答案

B

解析

数表的观察数表，可以发现规律：每一行都是等差数列，且第一行公差为1，第二行公差为2，第三行公差为4，-----，第2015行公差为，第2016行（最后一行）只有一个数为（1+2016）=，故选B。

考查方向

本题主要考查了数学归纳和猜想。

解题思路

观察数表，可以发现规律：每一行都是等差数列，且第一行公差为1，第二行公差为2，第三行公差为4，第2015行公差为，第2016行（最后一行）只有一个数，得出结果。

易错点

找不到规律。

知识点

等比数列的判断与证明

1

题型：单选题

|

单选题 · 5 分

6. 若成等比数列，则下列三个数：① ② ③，必成等比数列的个数为（）

A0

B1

C2

D3

正确答案

B

解析

由题可知：等比数列的相邻两项相乘仍然是等比数列。

A选项不正确，C选项不正确，D选项不正确，所以选B选项。

考查方向

本题主要考查等比数列的性质

解题思路

代入特值计算或由等比数列的基本性质，即可得到结果。

A选项不正确，C选项不正确，D选项不正确，所以选B选项。

易错点

本题易在代特值时发生错误。

知识点

平面向量数量积的运算等比数列的判断与证明

1

题型：填空题

|

填空题 · 5 分

6．设等比数列的前项的和为，若，则的值为_______

正确答案

63

解析

由等比数列前n项和的性质成等比数列，则成等比数列，，解得．

设等比数列{an}的首项为a1，公比为q．显然q≠1，由题意得

解之得：所以，

考查方向

本题主要考查等比数列的基本运算，等比数列的求和，考查学生的运算能力，难度中等.

解题思路

本题主要考查等比数列的基本运算，等比数列的求和。

解题步骤如下：利用公式或性质，列出等式。正确运算，得出结果。

易错点

本题易错点是公式会弄错，运算上出现错误。

知识点

等比数列的判断与证明

1

题型：单选题

|

单选题 · 5 分

9.在△ABC中，内角A，B，C 所对的边分别为 a，b，c，若 cos 2B＋cosB＝1－cos AcosC 则（）

Aa，b，c 成等差数列

Ba，b，c 成等比数列

Ca，2b，3c 成等差数列

Da，2b，3c 成等比数列

正确答案

B

解析

由cos 2B＋cosB＝1－cos AcosC

得到sin 2B=cos Acos C－cos（A＋C）

所以sin 2B=cos Acos C－cos AcosC＋sinAsinC

所以sin 2B=sinAsinC

由正弦定理得，b2 = ac，所以a，b，c 成等比数列，故选B。

考查方向

本题主要考查等比中项、同角三角函数的基本关系、两角和与差的余弦公式、正弦定理等知识，意在考查考生的运算推理能力。

解题思路

1.先利用三角函数中的公式将cos 2B＋cosB＝1－cos AcosC化简；

2.利用正弦定理得到边之间的关系即可。

易错点

1.对于题中cos 2B＋cosB＝1－cos AcosC的化简不会入手；

2.对于三角函数的化简出错

知识点

三角形中的几何计算等差数列的判断与证明等比数列的判断与证明

1

题型：简答题

|

简答题 · 14 分

某市2013年发放汽车牌照12万张，其中燃油型汽车牌照10万张，电动型汽车2万张．为了节能减排和控制总量，从2013年开始，每年电动型汽车牌照按50%增长，而燃油型汽车牌照每一年比上一年减少万张，同时规定一旦某年发放的牌照超过15万张，以后每一年发放的电动车的牌照的数量维持在这一年的水平不变．

（1）记2013年为第一年，每年发放的燃油型汽车牌照数构成数列，每年发放的电动型汽车牌照数构成数列，完成下列表格，并写出这两个数列的通项公式；

（2）从2013年算起，累计各年发放的牌照数，哪一年开始超过200万张？

正确答案

（1）

当且时，；

当且时，．而，

（2）当时，．

当时，

由得，

即，

解得

到2029年累积发放汽车牌照超过200万张

解析

本题属于数列的应用题，题目的难度是中等，本题的关键是：

（1）、从所给的数列中找出规律，并求出两数列的通项公式；

（2）、再根据数列的通项公式的分段函数性质，求出各自的前n项和，最后利用函数的性质给出答案。这类数列的应用题型较为常见。

考查方向

本题考查了数列与函数之间的综合应用，特别是分段函数与数列的应用

易错点

1、分类讨论：和的区别2、分类讨论的前n项和与的前n项和

知识点

等差数列的判断与证明等比数列的判断与证明分组转化法求和数列与不等式的综合

1

题型：简答题

|

简答题 · 18 分

已知函数（为常数，且），且数列是首项为4，公差为2的等差数列.

（1）求证：数列是等比数列；

（2）若，当时，求数列的前项和的最小值；

（3）若，问是否存在实数，使得是递增数列？若存在，求出的范围；若不存在，说明理由．

正确答案

(1) 证：由题意，

即，

∴

∴.

∵常数且，∴为非零常数，

∴数列是以为首项，为公比的等比数列.

(2) 当时， , ，

所以

因为,所以，是递增数列，

因而最小值为

(3) 由(1)知，，要使对一切成立，

即对一切成立.

当时，，对一切恒成立；

当时，，对一切恒成立，只需，

∵单调递增，

∴当时，.

∴，且，

∴.

综上所述，存在实数满足条件.

解析

本题属于数列与不等式的综合应用题，题目的难度是偏难，本题的关键是：

（1）、利函数的性质求出数列的通项公式；

（2）、利用等比数列的求和公式求出前n项和的表达式，并求出最小值；

（3）、根据数学归纳法，分类讨论出k的取值范围。

考查方向

本题考查了数列的综合应用题，特别是数列与不等式之间的应用题

易错点

1、由，得出.不容易想到2、对的讨论求出最小值讨论需要仔细3、数学归纳法的应用需要注意细节

知识点

等比数列的判断与证明数列与函数的综合数列与不等式的综合

1

题型：简答题

|

简答题 · 12 分

18．设数列{an}的前n项和为Sn，己知a1=l，nan+1=(n+2)Sn，n∈N*.

（1）求证：是等比数列；

（2）设Tn= S1+S2+--+Sn，求证：(n+l) Tn<nSn+1．

正确答案

（1）；

（2）略．

解析

试题分析：本题属于数列中的基本问题，题目的难度是逐渐由易到难．

（1）由已知得。

所以是以1为首项，2为公比的等比数列。

（2）由上知。

……①

……②

①-②得：。

即(n+l) Tn<nSn+1．

考查方向

本题考查了数列的问题．属于高考中的高频考点。

解题思路

本题考查数列问题，解题步骤如下：

（1）利用等比数列的定义证明。

（2）利用错位相减法求和。

易错点

错位相减法求和时相减的结果项数易错。

知识点

等比数列的判断与证明数列与不等式的综合

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点