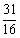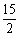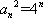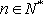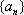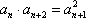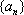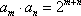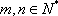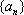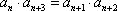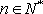- 等比数列的判断与证明
- 共122题
在等比数列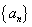
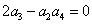
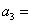
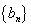
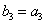
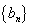
正确答案
2;10
解析
略
知识点
已知等比数列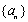
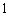
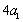
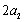
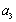
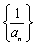
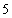
正确答案
解析
略
知识点
已知数列







(1)判断数列

(2)求
正确答案
见解析。
解析
(1)




所以




(2)由(1)可知







知识点
若函数


(1)判断下列函数:①

(2)证明:对任意的正奇数

(3)证明:任意的

正确答案
见解析
解析
(1)①②都是等比源函数.
(2)证明:假设存在正整数




等式两边同除以

因为
所以等式
所以假设不成立,说明对任意的正奇数

(3)因为任意的

所以任意的



由



令

所以
所以任意的


所以任意的

知识点
各项均为正数的等比数列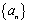
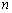
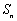
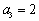
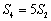
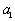
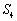
正确答案
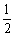
解析
略
知识点
从数列

(1)写出数列
(2)若




正确答案
见解析
解析
(1)
(2)证明:假设能抽出一个子列为无穷等差数列,设为



(i)当


所以


令

即存在


(ii)当


所以


因为d为正的常数,且
所以存在正整数m使得
令

因为

所以


综上,所以数列
知识点
设

正确答案
解析
略
知识点
已知等比数列



正确答案
9
解析
略
知识点
设数列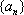
正确答案
解析
略
知识点
设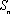
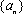

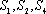
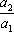
正确答案
解析
略
知识点
扫码查看完整答案与解析