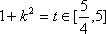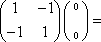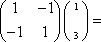- 直线与圆锥曲线的位置关系
- 共144题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
(1)
(2)
(3)
正确答案
见解析。
解析
(1)由题意可知,
令 
又





又
故
(2)用反证法证明
假设数列






两边同乘3t t2t-r,化简得3t-r+22t-r=2*2t-r3t-s
由于

(3)解法一:由(2)知:当

令
当

令
即 
将上述
整理得
解法二:用数学归纳法证明
(1) 当


(2) 假设
那么
由(2)知:当
令
令
就是说, 当
根据(1)和(2),可知不等式对任何
知识点
已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足
(1)求曲线C的方程;
(2)动点Q(x0,y0)(-2<x0<2)在曲线C上,曲线C在点Q处的切线为l,问:是否存在定点P(0,t)(t<0),使得l与PA,PB都相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值;若不存在,说明理由。
正确答案
见解析
解析
(1)由

得

由已知得
化简得曲线C的方程:x2=4y.
(2)假设存在点P(0,t)(t<0)满足条件,
则直线PA的方程是
曲线C在点Q处的切线l的方程是

由于-2<x0<2,因此-1<
①当-1<t<0时,

②当t≤-1时,

所以l与直线PA,PB一定相交。
分别联立方程组
解得D,E的横坐标分别是

则xE-xD=(1-t)
又|FP|=-


又
于是
=
对任意x0∈(-2,2),要使
解得t=-1.此时
故存在t=-1,使得△QAB与△PDE的面积之比是常数2.
知识点
在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由;
(3)若点M的横坐标为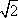


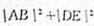
正确答案
见解析。
解析
(1)F抛物线C:x2=2py(p>0)的焦点F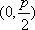
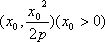
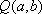
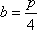

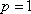

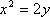
(2)假设存在点M,使得直线MQ与抛物线C相切于点M,
而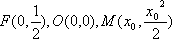
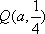
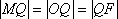
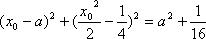
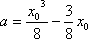
由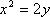
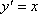
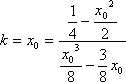
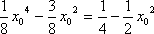
即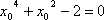
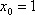
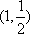
(3)若点M的横坐标为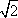
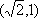
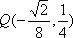
由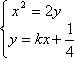
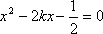
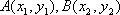
圆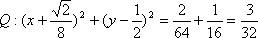
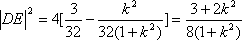
于是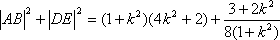
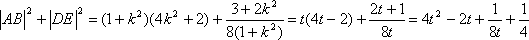
设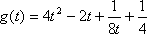
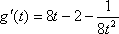
当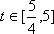
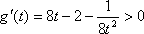
即当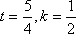
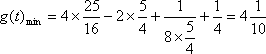
故当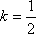
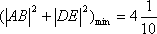
知识点
如图,双曲线

(1)双曲线的离心率e= _________ ;
(2)菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值
正确答案
(1)
(2)
解析
(1)直线B2F1的方程为bx﹣cy+bc=0,所以O到直线的距离为
∵以A1A2为直径的圆内切于菱形F1B1F2B2,
∴
∴bc=a2
∴(c2﹣a2)c2=a4
∴c4﹣a2c2﹣a4=0
∴e4﹣e2﹣1=0
∴
(2)菱形F1B1F2B2的面积S1=2bc
设矩形ABCD,BC=2m,BA=2n,∴
∵m2+n2=a2,∴
∴面积S2=4mn=
∴

∵bc=a2=c2﹣b2
∴
∴
知识点
正方形的四个顶点


正确答案

解析
∵A(﹣1,﹣1),B(1,﹣1),C(1,1),D(﹣1,1),
∴正方体的ABCD的面积S=2×2=4,
根据积分的几何意义以及抛物线的对称性可知阴影部分的面积S=2





则由几何槪型的概率公式可得质点落在图中阴影区域的概率是
知识点
已知x>0, y>0,证明:(1+x+y2)( 1+x2+y)≥9xy.
正确答案
见解析。
解析
因为x>0, y>0, 所以1+x+y2≥

所以(1+x+y2)( 1+x2+y)≥
知识点
在平面直角坐标系







正确答案
解析
目标函数即



知识点
已知矩阵M=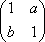
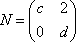
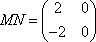
(1)求实数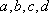
(2)求直线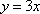
正确答案
见解析。
解析
(1)由题设得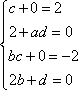
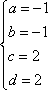
(2)因为矩阵M所对应的线性变换将直线变成直线(或点),所以可取直线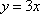
由
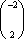
直线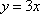
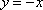
知识点
扫码查看完整答案与解析