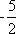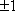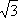- 直线与圆锥曲线的位置关系
- 共144题
8.已知定义域为







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
若变量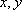
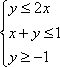
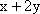
正确答案
解析
略
知识点
设关于x,y的不等式组
正确答案
解析
图中阴影部分表示可行域,要求可行域内包含y=



知识点
如图,直三棱柱



(1)证明:
(2)求二面角
正确答案
见解析
解析
(1)在
得:
同理:
得:
(2)
取










且

设

既二面角
知识点
设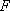
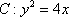

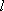
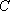
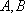
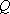
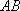
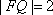
正确答案
解析
由已知得到: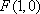
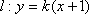
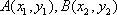
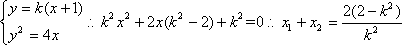
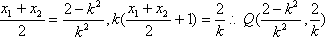
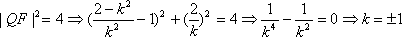
知识点
直线

正确答案
解析
略
知识点
假设每天从甲地去乙地的旅客人数


(1)求
(参考数据:若




(2)某客运公司用








正确答案
(1)0.977 2;(2)A型车5辆、B型车12辆
解析
(1)由于随机变量X服从正态分布N(800,502),
故有μ=800,σ=50,P(700<X≤900)=0.954 4.
由正态分布的对称性,可得
p0=P(X≤900)=P(X≤800)+P(800<X≤900)
=
(2)
设A型、B型车辆的数量分别为x,y辆,则相应的营运成本为1 600x+2 400y.
依题意,x,y还需满足:x+y≤21,y≤x+7,P(X≤36x+60y)≥p0.
由(1)知,p0=P(X≤900),
故P(X≤36x+60y)≥p0等价于36x+60y≥900.
于是问题等价于求满足约束条件
且使目标函数z=1 600x+2 400y达到最小的x,y.
作可行域如图所示,可行域的三个顶点坐标分别为P(5,12),Q(7,14),R(15,6)。
由图可知,当直线z=1 600x+2 400y经过可行域的点P时,直线z=1 600x+2 400y在y轴上截距
故应配备A型车5辆、B型车12辆
知识点
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等,设OAn=an.若a1=1,a2=2,则数列{an}的通项公式是__________。
正确答案
解析


∵a1=1,a2=2,OAn=an,
∴OA1=1,OA2=2.
又易知△OA1B1∽△OA2B2,
∴
∴

∵所有梯形AnBnBn+1An+1的面积均相等,
且△OA1B1∽△OAnBn,
∴


知识点
设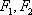
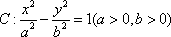
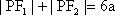
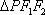
正确答案
解析
略
知识点
已知函数




(1)求函数

(2)求当


(3)是否存在




正确答案
见解析。
解析
(1)


所以,函数



(2)因为
所以,当



(3)考虑函数


则
当


当

当


所以,当


当且仅当

所以,
而
令

两式相减得,

所以,
故
所以,
当且仅当

所以,存在唯一一组实数

使得等式
知识点
扫码查看完整答案与解析