- 直线与圆锥曲线的位置关系
- 共144题
如图,在正方形














(1)求证:点

(2)过点







正确答案
(1)

解析
(1)依题意,过



设






(2)依题意:直线

由
此时


设:
又
分别带入
直线


知识点
如图,设椭圆C:

(1) 已知直线


(2) 若过原点





正确答案
见解析
解析
(1)方法1:设直线l的方程为

由于直线l与椭圆C只有一个公共点P,故△=0,即
又点P在第一象限,故点P的坐标为
方法2:作变换


切点




在圆



由
即

所以

即


利用逆变换
(2)由于直线l1过原点O且与直线l垂直,故直线l1的方程为x+ky=0,所以点P到直线l1的距离

因为
当且仅当
所以,点P到直线
知识点
已知椭圆

正确答案
解析
知识点
已知椭圆

(1)求椭圆
(2)直线







正确答案
(1)
(2)
解析
(1)因为椭圆
一内角为
所以


(2)设



当直线



所以
因为
所以



当直线


所以
当
方程有两个不同的解
又

所以


代入

又原点到直线的距离为
所以
化简得到
因为



综上,

知识点
已知椭圆的中心在原点,焦点在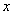
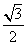
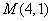
直线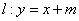
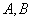
(1)求椭圆的方程;
(2)若直线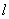
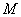
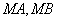
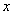
正确答案
见解析。
解析
知识点
已知椭圆



(1)求椭圆
(2)过点









正确答案
(1)
(2)
解析
(1)依题意不妨设



由


解得
所以椭圆

(2)依题直线

由

设



所以弦

所以

直线

由


所以
所以
又因为

所以
所以

知识点
已知中心在原点的双曲线



正确答案
解析
B;依题意




知识点
有一个半径为

正确答案
解析
略
知识点
将函数

正确答案
解析
略。
知识点
已知:椭圆





(1)求椭圆的方程;
(2)斜率大于零的直线过




(3)是否存在实数






正确答案
见解析
解析
(1)由



所以椭圆方程是:
(2)设EF:



设



由

得


直线


(3)将


记







解得



知识点
扫码查看完整答案与解析