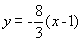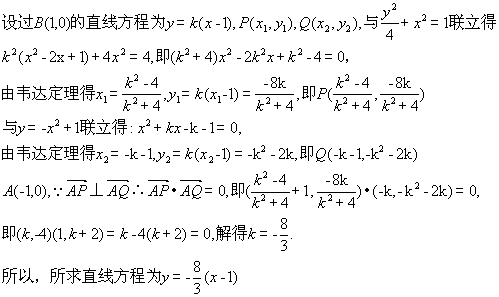- 直线与圆锥曲线的位置关系
- 共144题
11.双曲线





正确答案
解析
双曲线的渐近线方程为


因为


由


由

整理得,

应选B.
考查方向
解题思路
1.列方程组求出P点坐标;
2.由
易错点
1.易混淆焦点在X轴与Y轴的双曲线的渐近线方程;
2.解包含有字母系数的方程组时,易出错。
知识点
9.已知直线:


正确答案
解析
直线:y=kx-k+1恒过定点(1,1),利用直线:y=kx-k+1与曲线C:
考查方向
曲线与方程
解题思路
根据等量关系,建立方程,然后求出参数的取值范围
易错点
计算化简错误
知识点
11.过点






正确答案
解析
过点


解得
考查方向
解题思路
因为双曲线是无限接近于它的渐近线的,所以双曲线到直线的距离恒大于
易错点
不能将曲线到直线的距离转化成直线到直线的距离,导致计算繁琐甚至出错
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图,曲线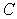
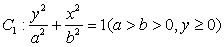
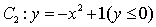
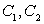
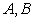
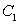
(1)求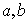
(2)过点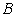
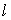
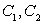
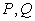
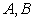
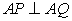
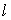
正确答案
(1) a=2,b=1 (2)
解析
(1)
(2)
知识点
甲厂以x 千克/小时的速度运输生产某种产品(生产条件要求

(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润。
正确答案
见解析。
解析
(1)根据题意,
又
(2)设利润为
故

知识点
若曲线


正确答案
解析
曲线







知识点
11. 设双曲线





正确答案
解析
设边长为
由于离心率
所以

而
由于双曲线的离心率e>1,所以

考查方向
解题思路
在三角形中,利用余弦定理,判断边
易错点
此题容易在双曲线的离心率与方程中a、b、c的关系上出错;余弦定理应用时出错;再者就是计算失误
知识点
9.已知











正确答案
解析
延长













考查方向
解题思路
由


易错点
对相关知识不熟悉导致出错。
知识点
20. 如图,双曲线






(1)当直线



正确答案
2
右支上不存在
解析
双曲线的焦点在















当直线











设直线























考查方向
解题思路
先求出焦点坐标以及直线


写出直线




设直线




则








易错点
计算要仔细。
①计算要准确仔细②注意计算技巧
知识点
扫码查看完整答案与解析