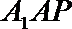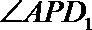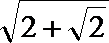- 直线、平面平行的判定与性质
- 共628题
20.已知数列{an}中,a1=2,a2=3,其前n项和Sn满足Sn+1+Sn-1=2Sn+1(n≥2,n∈N*).
(1) 求数列{an}的通项公式;
(2) 设
正确答案
(1) 由已知,



即


且
∴ 数列

∴
(2) ∵
∴
要使
即
∴
即
1'当

∵当且仅当

∴λ<1;
2'当

∵当且仅当


∴λ>-2.
故-2<λ<1,又λ为非零整数,
则λ=-1.
综上所述,存在λ=-1,使得对任意

解析
解析已在路上飞奔,马上就到!
知识点
9. 一个四棱锥的三视图如图所示,其侧视图是等边三角形。该四棱锥的体积等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.下列命题中的真命题为______________________
(1) 复平面中满足|z-2|-|z+2|=1的复数
(2) 当

(3)已知函数



(4)在平面直角坐标系


(5) 设平面直角坐标系xoy中方程F(x,y)=0表示一个椭圆,则总存在实常数p、q,使得方程F(px , qy)=0表示一个圆。
正确答案
(2)(3)(4)
解析
解析已在路上飞奔,马上就到!
知识点
7. 过点(0,1)引x2+y2-4x+3=0的两条切线,这两条切线夹角的余弦值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.对于事件A,P(A)表示事件A发生的概率。则下列命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,五面体





(I)求这个几何体的体积;
(Ⅱ)




(III)求二面角
正确答案
解: (I)显然这个五面体是四棱锥









(Ⅱ)当



证明:连结

∵四边形


∵

且


∴



(III)建立空间直角坐标系
则



所以





则有

可得平面

设


令



所以二面角
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如果函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,棱长为


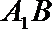
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在三棱锥









(1)求证:
(2)求二面角
正确答案
解:
(1)连结PD,






又




(2)法一:




则DE


DE
过D做DF垂直PB与F,连接EF,则EF 
∠DFE为所求二面角的平面角
则:DE=



法二:




如图,以D为原点建立空间直角坐标系








设平面PBE的法向量

得




设二面角的

由图知,
所以

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析