- 直线、平面平行的判定与性质
- 共628题
16.在四棱锥P-ABCD中,∠ACD=90°,∠BAC=∠CAD,PA⊥平面ABCD,E为PD的中点。
(1)求证:平面PAC⊥平面PCD;
(2)求证:CE//平面PAB。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知y=

正确答案
1
解析
∵ f(x)是奇函数,且当x∈(-2,0)时,f(x)的最小值为1,
∴f(x)在(0,2)上的最大值为-1.
当x∈(0,2)时,
令f'(x)=0,得x=
又
∴
当

当
f'(x)<0,f(x)在
∴f(x)max=
解得a=1.
知识点
18.在多面体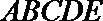
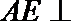
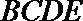
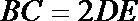
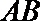
(I)求证: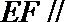
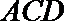
(II)若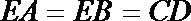
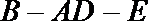
正确答案
证明:(Ⅰ)取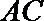
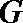
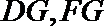
因为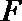
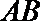
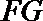
则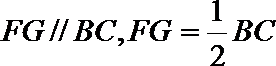
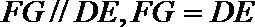
则四边形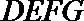
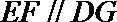
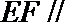
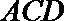
(Ⅱ)过点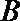
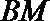
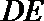
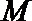
因为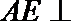
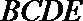
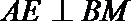
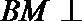
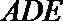
过
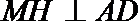

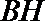
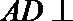
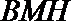
所以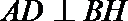
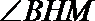
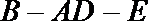
设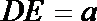
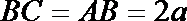
在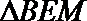
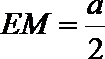
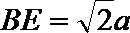
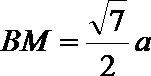
又因为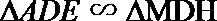
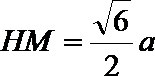
解析
解析已在路上飞奔,马上就到!
知识点
22. 如图,在直三棱柱




(1)设




(2)若点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.某几何体的三视图如图所示,则它的体积是_______.
正确答案
解析
由三视图可知此几何体是一个正方体上面放置一个底面半径为1的圆锥,其体积V=V正方体+V圆锥=23+


知识点
9.如图,空间四边形ABCD的对棱AD与BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于点E、F、G、H,则截面EFGH的最大面积为____________.
正确答案
解析
∵ AD与BC成60°的角,
∴ ∠HEF=60°或120°.
设 =
∴ 
∴ EF=ax,由
得EH=a(1-x).
∴ S四边形EFGH=EF·EH·sin 60°=
当

∴ 即当E为AB的中点时,截面的面积最大,最大面积为
知识点
21.已知

(1)若

(2)求证:对任意
正确答案
(1)依题意





所以

(2)
设
则
考虑到

又当


所以对任意
解析
解析已在路上飞奔,马上就到!
知识点
25.已知






正确答案
略
解析
试题分析:本题属于立体几何中的基本问题,题目为容易题.
证明:在


又因为

所以四边形
所以
又因为


考查方向
本题考查了立体几何中的线面平行的问题.属于高考中的高频考点。
解题思路
本题考查线面平行,解题步骤如下:
找出平行四边形即可
易错点
容易与线面垂直混淆。
知识点
5.如图,在四棱柱





正确答案
解析
利用线面平行的判定定理,需在平面


解题思路
(1)线面平行的证明方法:利用线面平行的判定定理转化成线线平行来证,难点是符合要求线的选取;转换成面面平行来证,首先要做的是找到符合面面平行判定定理的两对相交直线(2)二面的求法:转化成线线角,难点是这两条合适线的选取;(3)空间向量求角有明显的优势,不需要找角,但要建好坐标系,求好法向量和方向向量。
易错点
(1)找不到与
(2)找不到平面

(3)用空间向量解答时建系错误,如以






教师点评
数学思想方法是数学知识在更高层次上的抽象与概括,它蕴含在数学知识发生、发展和应用的过程中,是由知识向能力转化的重要桥梁。本题既考查了空间想象能力,又运用了转化与化归思想,设计门槛低、入口宽,运用的思想方法有层次、有梯度,从而有效地区分不同层次考生的能力水平。这样的设计,体现了以知识为载体,以方法为依托,以考查能力为目的的考查要求,提高了试题的区分度,有利于高校选拔人才。
知识点
16.在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2
(1)求证:AC⊥PB;
(2)若PC=2,点M是棱PB上的点,且CM∥平面PAD,求BM的长。
正确答案
见解析
解析
(1)∵PC⊥平面ABCD,∴PC⊥AC,
又∠CBA=30°,BC=2
∴AC=
=
∴AC2+BC2=4+12=16=AB2,∴∠ACB=90°,
故AC⊥BC.又∵PC、BC是平面PBC内的两条相交直线,
故AC⊥平面PBC,∴AC⊥PB.
(2) BM=2
考查方向
解题思路
(1)由余弦定理求AC
(2)由勾股逆定理得∠ACB=90°
(3)AC⊥BC,PC⊥AC,AC⊥平面PBC,∴AC⊥PB
易错点
证明过程不到位。
知识点
扫码查看完整答案与解析