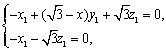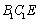- 直线、平面平行的判定与性质
- 共628题
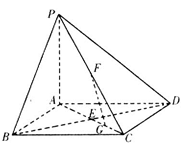
如图,在底面是正方形的四棱锥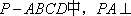
(1)求证: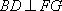
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由;
(3)当二面角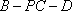
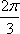
正确答案
见解析
解析
知识点
设m,n是两条不同的直线,

正确答案
解析
略
知识点
双曲线






正确答案
解析
略
知识点
如图,平面ABB1A1为圆柱OO1的轴截面,点C为
(1)求证:B1M∥平面O1AC;
(2)若AB=AA1,∠CAB=30°,求二面角C-AO1 -B的余弦值。
正确答案
见解析
解析
知识点
如图,在四棱锥






(1)求证:

(2)求二面角
正确答案
见解析。
解析
证明(1)连结














(2)

















则









由

设平面

由


设平面


由



设二面角




知识点
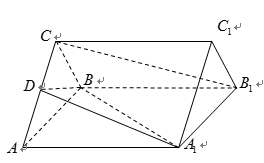
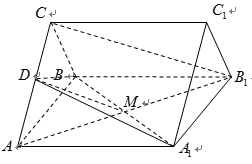
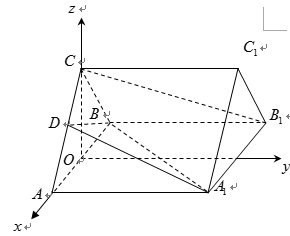
如图,正三棱柱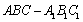
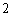
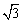
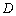
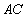
(1)求证: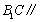
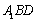
(2)求二面角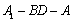
(3)在线段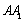
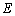
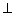
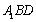
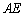
正确答案
见解析
解析
(1)证明:连结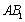
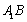
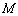
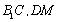
因为三棱柱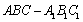
所以四边形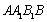
所以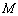
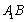
因为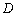
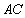
所以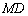
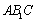
所以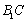
因为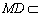
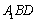
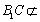
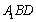
所以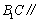
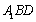
(2)解:作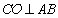
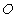
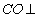
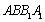
所以在正三棱柱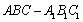
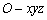
因为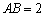
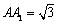

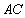
所以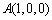
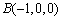
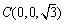
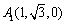
所以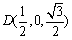
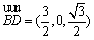
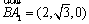
设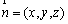
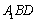
所以
令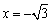
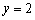
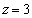
所以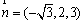
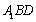
由题意可知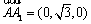
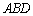
所以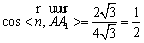
所以二面角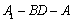
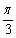
(3)设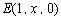
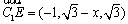
设平面
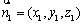
所以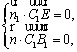
令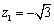
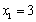
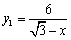
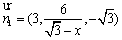
又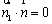
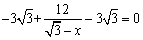
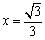
所以存在点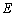
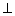

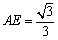
知识点
如图,在正三棱柱





正确答案
解析
略
知识点
极坐标方程


正确答案
解析
略
知识点
如图,四棱锥









(1)求证:

(2)设二面角



正确答案
见解析
解析
(1)由



又









解得:


所以



设面



因为




(2)设面



所以






知识点
如图几何体中,四边形





(1)若



(2)求二面角
正确答案
见解析
解析
(1)连接




因为点



所以




所以

(2)取





所以
作












又





以








设面

由

设面

由

设二面角

则
知识点
扫码查看完整答案与解析