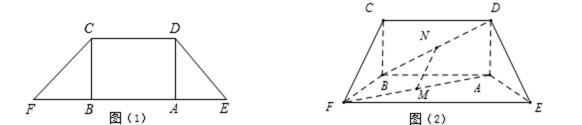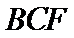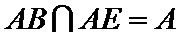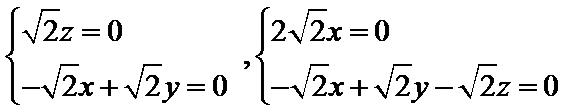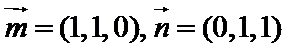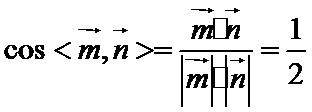- 直线、平面平行的判定与性质
- 共628题
如图,在三棱柱








22.求

23.求证:

24.求三棱锥
正确答案
见解析
解析
证明:∵底面三边长













考查方向
解题思路
第一问由线面垂直证明线线垂直,第二问由线线平行证明线面平行,第三问根据三棱锥体积的计算公式,先求出三棱锥底面面积,再找到高,进而求解。
易错点
直线与平面的关系的判断与证明,逻辑错误
正确答案
见解析
解析
证明:设







∴






考查方向
解题思路
第一问由线面垂直证明线线垂直,第二问由线线平行证明线面平行,第三问根据三棱锥体积的计算公式,先求出三棱锥底面面积,再找到高,进而求解。
易错点
直线与平面的关系的判断与证明,逻辑错误
正确答案
见解析
解析
解:取


∵



又∵



∴

∵
∴
考查方向
解题思路
第一问由线面垂直证明线线垂直,第二问由线线平行证明线面平行,第三问根据三棱锥体积的计算公式,先求出三棱锥底面面积,再找到高,进而求解。
易错点
直线与平面的关系的判断与证明,逻辑错误



18.若平面


19.求平面
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
确定线面平行判定的方式:线//面→线//线
由已知AD//BC,得到线//面
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
根据线//面→线//线
根据已知条件建立坐标系,并标记所需点的坐标
计算相应面的法向量,并求向量的夹角
判断两面角的大小确定二面角
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
已知平行四边形ABCD中,AB=4,E为 AB的中点,且△
22.F 是线段A1 C的中点,求证:BF //平面A1 DE ;
23.求证:A 1 D⊥CE ;
24.求点A1到平面BCDE的距离.
正确答案
见解析
解析
考查方向
解题思路
第一问根据特殊四边形的相关性质进行证明,第二问利用线面垂直证明线线垂直,第三问用和空间距离相关的性质求解。
易错点
辅助线作不出来;立体感不强
正确答案
见解析
解析
考查方向
解题思路
第一问根据特殊四边形的相关性质进行证明,第二问利用线面垂直证明线线垂直,第三问用和空间距离相关的性质求解。
易错点
辅助线作不出来;立体感不强
正确答案
见解析
解析
考查方向
解题思路
第一问根据特殊四边形的相关性质进行证明,第二问利用线面垂直证明线线垂直,第三问用和空间距离相关的性质求解。
易错点
辅助线作不出来;立体感不强
8.设m,n是两条不同的直线,

正确答案
解析
若α∥β,m∥α,n∥β,则



考查方向
解题思路
1)分析判断各选项的正确性;
2)得出结论.
易错点
本题易在判断选项B出现错误,易忽视判断线线垂直的充分条件.
知识点
如图,在三棱锥P-AMC中,AC=AM=PM,AM⊥AC,PM⊥平面AMC,B,D分别为CM,AC的中点.
22.在PD上确定一点N,使得直线PM∥平面NAB,并说明理由;
23.在(Ⅰ)的条
正确答案
(Ⅰ)N为PD靠近D的一个三等分点;
解析
试题分析:本题属于立体几何的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意空间直角坐标系的建立;
(Ⅰ)N为PD靠近D的三等分点.理由如下:
取PC的中点E,连接BE,
由于B,E分别为CM,PC的中点,所以BE∥PM,
又BE

所以直线PM∥平面ABE,
连接AE,交PD于N点,即为满足条件的点.
由于AE,PD分别是
所以AE和PD的交点N为
故N为PD靠近D的一个三等分点.
考查方向
解题思路
本题考查线面平行的判定、利用空间向量求二面角,解题步骤如下:
1)取中点,利用三角形的中位线证明线线平行;
2)连接AE,交PD于N点,即为满足条件的点,得到所求点的位置;
3)建立空间直角坐标系;
4)利用空间向量求二面角。
易错点
1、建立空间直角坐标系前没有证明垂直关系.
正确答案
(Ⅱ)
解析
试题分析:本题属于立体几何的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意空间直角坐标系的建立;
(Ⅱ)因为AC=AM,AM⊥AC,所以

所以C(


即

因为PM⊥平面AMC,由(Ⅰ)知BE∥PM,
所以BE⊥平面AMC,则CM⊥BE.
又AC=AM,B为CM的中点,则CM⊥AB,
所以CM⊥平面NAB,
所以可取平面NAB的一个法向量为
设平面PAC的法向量
由


可得平面PAC的一个法向量
由

所以平面NAB和平面PAC所成锐二面角α的大小为
考查方向
解题思路
本题考查线面平行的判定、利用空间向量求二面角,解题步骤如下:
1)取中点,利用三角形的中位线证明线线平行;
2)连接AE,交PD于N点,即为满足条件的点,得到所求点的位置;
3)建立空间直角坐标系;
4)利用空间向量求二面角。
易错点
1、建立空间直角坐标系前没有证明垂直关系.
如图,在四棱锥





19.求证:
20.若平面



正确答案
(1)

解析
试题分析:本题属于立体几何线面平行证明及二面角的余弦值的求解问题,属于中档题。
(Ⅰ)证明:取




∴
∵
∴
∵




∴平面

∵
∴

考查方向
解题思路
(1)通过面面平行证明线面平行;
(2)根据已知条件建立空间直角坐标系,用空间向量的方法求二面角的余弦值。
易错点
1)证明过程遗漏直线相交的条件
2)没有描述建系的依据,或点的坐标出错或运算出错。
正确答案
(2)所求二面角的余弦值为
解析
试题分析:本题属于立体几何线面平行证明及二面角的余弦值的求解问题,属于中档题。
(Ⅱ)解:









如图所示.
则点




设平面
则

设平面
因此所求二面角的余弦值为
考查方向
解题思路
(1)通过面面平行证明线面平行;
(2)根据已知条件建立空间直角坐标系,用空间向量的方法求二面角的余弦值。
易错点
1)证明过程遗漏直线相交的条件
2)没有描述建系的依据,或点的坐标出错或运算出错。
5.已知

正确答案
解析
对于选项A.


对于选项C.,直线

考查方向
解题思路
根据选项逐个进行分析、判断。
易错点
对线面、面面的平行或垂直的判定定理理解不透彻,导致出错。
知识点
如图,菱形




22.求证:

23.若

正确答案
见解析
解析
图,过点




















考查方向
解题思路
解题步骤如下:由平面




易错点
本题易在证明线面垂直、平行或求锥体的体积时发生错误 。
正确答案
几何体
解析
连接





















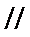





考查方向
解题思路
解题步骤如下:由于该几何体比较复杂,需要分成2个几何体来求解,根据题目给出的条件,求出每个几何体的底面积和对应的高,即可得到几何体的体积。
易错点
本题易在证明线面垂直、平行或求锥体的体积时发生错误 。
如图,多面体ABCDPE的底面ABCD是平行四边形,


20.若棱AP的中点为H,证明: HE∥平面ABCD
21.求二面角
正确答案
(1)略;
解析
(1)∵底面ABCD是平行四边形,

所以HE∥GC,HE

考查方向
解题思路
1)第一问通过平行四边形得到线线平行,由线面平行的判定定理得到线面平行;
2)第二问建立空间直角坐标系,求出两个面的法向量,再求出二面角的平面角。
易错点
直接找二面角,会出现找不到面的垂线的错误,若用空间向量,能得到两个面的向量的夹角,但是向量的夹角不一定是二面角的平面角。
正确答案
(2)
解析
(2)法一:如图,取PB的中点M,连接AC,DB交于点F,连接ME,MF,作FK⊥PB于点K,容易得到∠AKF是二面角A-PB-D的平面角




从而
由于点M是PB的中点,所以MF是△PDB的中位线,MF∥PD,且


故二面角
法二:由(1)知,DA,DC,DP两两互相垂直,建立空间直角坐标系
设平面PBE的法向量为








所以
从图形可知,二面角A-PB-E是钝角,所以二面角A-PB-E的大小为
考查方向
解题思路
1)第一问通过平行四边形得到线线平行,由线面平行的判定定理得到线面平行;
2)第二问建立空间直角坐标系,求出两个面的法向量,再求出二面角的平面角。
易错点
直接找二面角,会出现找不到面的垂线的错误,若用空间向量,能得到两个面的向量的夹角,但是向量的夹角不一定是二面角的平面角。
如图(1),在等腰梯形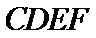
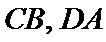

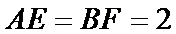
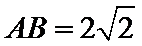
现将梯形沿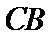
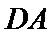
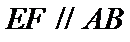
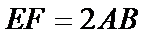
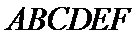
图(2)示,已知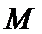
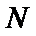
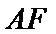
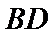
18.求证: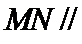
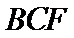
19.若直线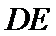
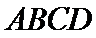
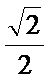
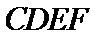
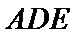
正确答案
见解析
解析
(Ⅰ)证明:连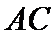
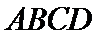
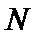
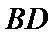
∴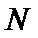
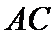
在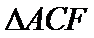
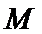
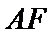
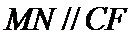
∵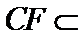
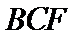
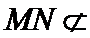
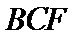
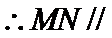
考查方向
解题思路
连结AC,通过证明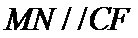
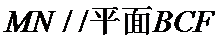
易错点
主要易错于线面角的判断出错,
正确答案
见解析
解析
(Ⅱ)依题意知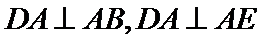
∴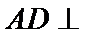
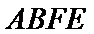
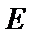
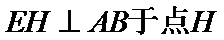
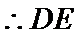
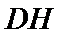
所以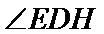
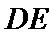
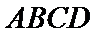
所以:
所以:
设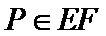
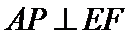
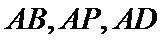

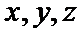
则
设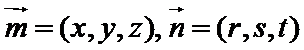
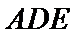
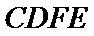
令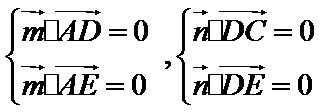
即
取
则
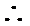
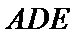
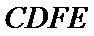
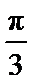
考查方向
解题思路
先由线面垂直的判定定理可证得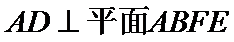
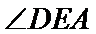
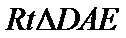
分别以AB,AP,AD所在的直线建立空间直角坐标系,求出平面ADE与平面CDFE的法向量,代入向量夹角公式,可得答案.
易错点
主要易错于线面角的判断出错,
扫码查看完整答案与解析