- 相似三角形的性质
- 共31题
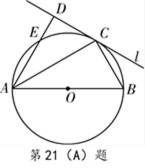
如图,圆O的直径AB=4,C为圆周上一点,BC=2,过C作圆O的切线l,过A作l的垂线AD,AD分别与直线l、圆O交于点D、E,求线段AE的长。
正确答案
见解析
解析
在Rt△ABC中,因为AB=4,BC=2,所以∠ABC=60°,
因为l为过C的切线,所以∠DCA=∠CBA,
所以∠DCA=∠ABC=60°,
又因为AD⊥DC,所以∠DAC=30°。
在△AOE中,因为∠EAO=∠DAC+∠CAB=60°,且OE=OA,
所以AE=AO=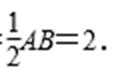
知识点
如图,AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB的延长线于点C,若DA = DC,求证:AB = 2 BC。
正确答案
见解析。
解析
连结OD,BD,
因为AB是圆O的直径,所以
因为DC是圆O的切线,所以
因为AD = DC,所以

即2OB = OB + BC,得OB = BC,故AB = 2 BC。
知识点
如图,M是平行四边形ABCD的边AB的中点,直线l过点M分别交AD,AC于点E,F,若AD=3AE,则AF:FC= 。
正确答案
1:4
解析
如图所示,设直线l交CD的延长线于点N。
∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD。
∵M是边AB的中点,∴
∴

故答案为1:4。
知识点
如图,⊙
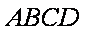


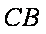
长线上一点,直线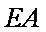
求证: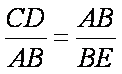
正确答案
见解析。
解析
连结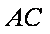
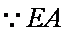
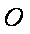
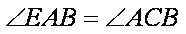
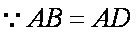
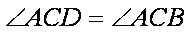
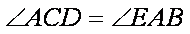

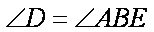
∴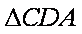
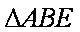
∴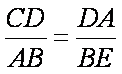
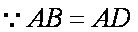
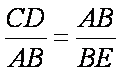
知识点
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB。
(1)证明:AC2=AD·AE
(2)证明:FG∥AC
正确答案
见解析。
解析
(1)∵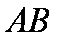

∴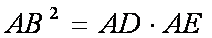
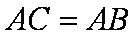
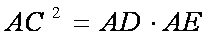
(2)∵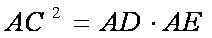
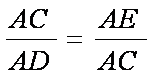

∴
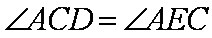
又∵四边形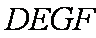

∴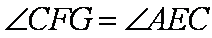
∴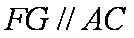
知识点
扫码查看完整答案与解析