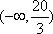利用基本不等式求最值
共114题

· 利用基本不等式求最值

利用基本不等式求最值
共114题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 5 分

设a＋b＝2，b＞0，则当a＝__________时，取得最小值。

正确答案

－2

解析

因为a＋b＝2，所以

1＝＝

≥，

当a＞0时，，；

当a＜0时，，，当且仅当b＝2|a|时等号成立。

因为b＞0，所以原式取最小值时b＝－2a.

又a＋b＝2，所以a＝－2时，原式取得最小值。

知识点

导数的几何意义导数的运算利用基本不等式求最值

题型：填空题

填空题 · 5 分

将边长为1m正三角形薄片，沿一条平行于底边的直线剪成两块，其中一块是梯形，记,则S的最小值是____▲____。

正确答案

解析

考查函数中的建模应用，等价转化思想。一题多解。

设剪成的小正三角形的边长为，则：

（方法一）利用导数求函数最小值。

，

当时，递减；当时，递增；

故当时，S的最小值是。

（方法二）利用函数的方法求最小值。

令，则：

故当时，S的最小值是。

知识点

解三角形的实际应用利用基本不等式求最值

题型：填空题

填空题 · 5 分

若存在实数满足，则实数的取值范围是。

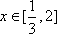
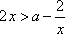
正确答案

解析

略。

知识点

利用基本不等式求最值

题型：单选题

单选题 · 5 分

已知a＞0，b＞0，a+b=2，则的最小值是

正确答案

解析

因为a+b=2，所以

知识点

利用基本不等式求最值

题型：填空题

填空题 · 5 分

设实数x,y满足3≤≤8，4≤≤9，则的最大值是 ▲ 。

正确答案

解析

考查不等式的基本性质，等价转化思想。

，，，的最大值是27。

知识点

利用基本不等式求最值

题型：简答题

简答题 · 14 分

某兴趣小组测量电视塔AE的高度H(单位：m），如示意图，垂直放置的标杆BC的高度h=4m，仰角∠ABE=，∠ADE=。

（1）该小组已经测得一组、的值，tan=1.24，tan=1.20，请据此算出H的值；

（2）该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离d（单位：m），使与之差较大，可以提高测量精确度。若电视塔的实际高度为125m，试问d为多少时，-最大？

正确答案

（1）124m.

（2）m

解析

（1），同理：，。

AD—AB=DB，故得，解得：。

因此，算出的电视塔的高度H是124m。

（2）由题设知，得，

，（当且仅当时，取等号）

故当时，最大。

因为，则，所以当时，-最大。

故所求的是m。

知识点

两角和与差的正切函数解三角形的实际应用利用基本不等式求最值

题型：单选题

单选题 · 5 分

已知两条直线和，与函数的图像从左至右相交于点，与函数的图像从左至右相交于点，记线段AC和BD在轴上的投影长度分别为，当m变化时，的最小值为

正确答案

解析

在同一坐标系中作出y=m，y=(m＞0)，图像如下图，

由= m，得，= ，得.

依照题意得.

，.

知识点

利用基本不等式求最值基本不等式的实际应用

题型：单选题

单选题 · 5 分

双曲线的离心率为2，则的最小值为（）

正确答案

解析

略。

知识点

利用基本不等式求最值双曲线的几何性质

继续学习学习下一知识点

下一知识点 : 不等式与函数的综合问题

百度题库 > 高考 > 理科数学 > 利用基本不等式求最值

扫码查看完整答案与解析