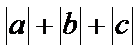- 利用基本不等式求最值
- 共114题
10. 已知(
正确答案
解析








故A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
含x2与x3的项的系数,再根据绝对值之比为1:6,算得
易错点
确定项的系数时计算易出错。
知识点
15.设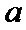
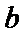
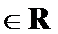
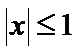
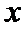
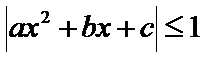
的最大可能值为______.
正确答案
3
解析
任意满足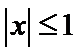
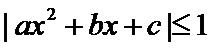
即有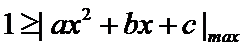
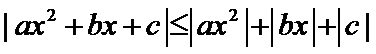
由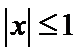
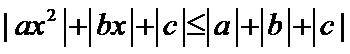
可得当且仅当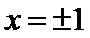
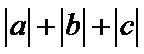
即有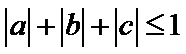
即有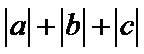
故答案为:1.
考查方向
解题思路
由题意可得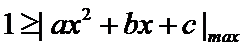
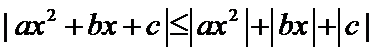
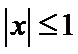
易错点
主要易错于不等式的转化,
知识点
14.若

正确答案
解析
由基本不等式得



考查方向
解题思路
利用基本不等式得到
易错点
找不到

知识点
7. 若不等式


正确答案
解析
由基本不等式得
(1)当



(2)当






(3)当







考查方向
解题思路
1.先利用基本不等式将题中给出的不等式转化为
2.利用分类讨论的思想求解出k的取值范围。
易错点
1.不知道分类的标准导致出现混乱;
2.不会分离常数求参数的取值范围。
知识点
9.一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c,


正确答案
解析
由题意可知 


考查方向
解题思路
根据题意可求3a+2b的值,然后构造基本不等式的形式求解问题答案
易错点
计算错误,活用“1”
知识点
6.设


正确答案
解析
1是a与b的等比中项,所以ab=1,所以当且仅当a=b=1时,原式有最小值,为2.所以选C
考查方向
本题主要考查等比数列,不等式相关考点,属于中等题
解题思路
先得出a,b的等量关系,然后直接应用基本不等式求最小值。
易错点
不理解等比中项,不会运用基本不等式求解问题
知识点
14.己知平行四边形的周长为6,则其对角线长的平方和的最小值是 .
正确答案
9
解析
试题分析:本题属于平面向量和基本不等式的问题,题目的难度较小。注意转化为平面向量求解。
考查方向
本题主要考查了平面向量和基本不等式的问题。
解题思路
本题考查平面向量,解题步骤如下:
设平行四边形的两邻边分别为向量a,b,夹角为θ。则对角线的平方和为(a+b)2+(a-b)2=2a2+2b2≥(a+b)2=9。
易错点
本题必须注意转化为平面向量的问题求解,忽视则会出现错误。
知识点
17.在

(1)求
(2)若


正确答案
(1)
(2)
解析
(1)由正弦定理知
即
(2)在

即


此时
考查方向
本题主要考查利用正(余)弦定理解三角形及其常用的三角恒等变换。
解题思路
(1)三角函数切化弦。
(2)第二问利用余弦定理结合基本不等式求解即可。
易错点
(1)三角公式不熟悉。
(2)第二问不会用基本不等式处理。
知识点
6.各项均为正数的等差数列


正确答案
解析
考查方向
解题思路
注意观察项数(下角标)的关系1+12=4+9。
易错点
无法充分利用条件,将条件引向结论。
知识点
(4分)(2015•上海)设f﹣1(x)为f(x)=2x﹣2+
正确答案
4
知识点
扫码查看完整答案与解析