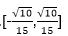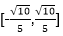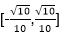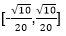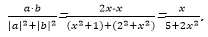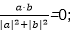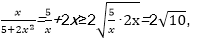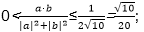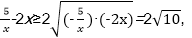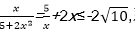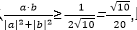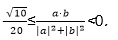利用基本不等式求最值
共114题

利用基本不等式求最值
共114题

热门试卷

题型：简答题

简答题 · 14 分

17．某商场为促销要准备一些正三棱锥形状的装饰品，用半径为10cm的圆形包装纸包装。要求如下：正三棱锥的底面中心与包装纸的圆心重合，包装纸不能裁剪，沿底边向上翻折，其边缘恰好达到三棱锥的顶点，如图所示。设正三棱锥的底面边长为xcm，体积为Vcm3 在所有能用这种包装纸包装的正三棱锥装饰品中，V的最大值是多少？并求此时x的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用基本不等式求最值棱柱、棱锥、棱台的体积

题型：填空题

填空题 · 5 分

7.设x,y均为正数,且,则xy的最小值为_________.

正确答案

解析

=去分母后为xy-7=3(x+y)≥6,解得xy≥49.

知识点

利用基本不等式求最值

题型：单选题

单选题 · 5 分

4.若直线通过点M(cos α,sin α),则的最小值为（　　　）

正确答案

解析

设向量m=(cos α,sin α),

由题意知=1,由m·n≤|m||n

可得1=

即的最小值是1,

故选B.

知识点

函数的值域利用基本不等式求最值

题型：填空题

填空题 · 5 分

9.已知点P(x,y)是椭圆上的一个动点,则x-y的最小值是_______.

正确答案

解析

根据题意,令=sin θ,所以可设动点P的坐标为(θ),其中0≤θ<2π.

因此

所以当时,
x-y取最小值.

知识点

函数的值域利用基本不等式求最值

题型：单选题

单选题 · 5 分

6.已知a=(x,1),b=(2,-x),那么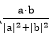的取值范围是（　　）

正确答案

解析

若x=0,

则

若x>0,由于

则

若x<0,由于

则

那么

即-

知识点

平面向量数量积的运算利用基本不等式求最值

题型：单选题

单选题 · 5 分

7．已知a > 0，b > 0，a、b的等差中项是，且，则x + y的最小值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用利用基本不等式求最值

题型：单选题

单选题 · 5 分

4．已知，现有下列不等式：

①；

②；

③；

④，

其中正确的是（）

A②④

B①②

C③④

D①③

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用对数值大小的比较不等式的性质利用基本不等式求最值

题型：单选题

单选题 · 5 分

6．各项均为正数的等差数列中，，则前12项和的最小值为（）

正确答案

解析

考查方向

本题主要考查等差数列的性质、求和公式，及均值不等式的应用。

解题思路

注意观察项数（下角标）的关系1+12=4+9。

易错点

无法充分利用条件，将条件引向结论。

知识点

等差数列的性质及应用利用基本不等式求最值

题型：单选题

单选题 · 5 分

2．函数的值域是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域利用基本不等式求最值

题型：填空题

填空题 · 4 分

7．若，且，则的最小值是___________．

正确答案

解析

∵，且

∴

（当且仅当即时，等号成立）

∴的最小值是16．

考查方向

本题考查基本不等式，是容易题．

解题思路

，展开，再利用基本不等式求得最小值，注意等号成立的条件．

易错点

当一个整数式子与一个分式式子在一个题中出现时，求一个式子的最值，常将两个式子相乘，展开，然后利用基本不等式求解．利用基本不等式求最值要注意：一正、二定、三相等．

知识点

利用基本不等式求最值

继续学习学习下一知识点

下一知识点 : 不等式与函数的综合问题

百度题库 > 高考 > 理科数学 > 利用基本不等式求最值

扫码查看完整答案与解析