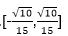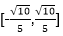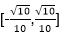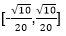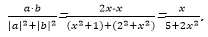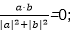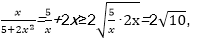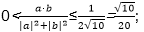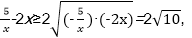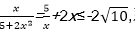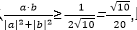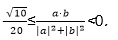利用基本不等式求最值
共114题

利用基本不等式求最值
共114题

热门试卷

题型：简答题

简答题 · 14 分

17．某商场为促销要准备一些正三棱锥形状的装饰品，用半径为10cm的圆形包装纸包装。要求如下：正三棱锥的底面中心与包装纸的圆心重合，包装纸不能裁剪，沿底边向上翻折，其边缘恰好达到三棱锥的顶点，如图所示。设正三棱锥的底面边长为xcm，体积为Vcm3 在所有能用这种包装纸包装的正三棱锥装饰品中，V的最大值是多少？并求此时x的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用基本不等式求最值棱柱、棱锥、棱台的体积

题型：填空题

填空题 · 5 分

7.设x,y均为正数,且,则xy的最小值为_________.

正确答案

解析

=去分母后为xy-7=3(x+y)≥6,解得xy≥49.

知识点

利用基本不等式求最值

题型：单选题

单选题 · 5 分

4.若直线通过点M(cos α,sin α),则的最小值为（　　　）

正确答案

解析

设向量m=(cos α,sin α),

由题意知=1,由m·n≤|m||n

可得1=

即的最小值是1,

故选B.

知识点

函数的值域利用基本不等式求最值

题型：填空题

填空题 · 5 分

9.已知点P(x,y)是椭圆上的一个动点,则x-y的最小值是_______.

正确答案

解析

根据题意,令=sin θ,所以可设动点P的坐标为(θ),其中0≤θ<2π.

因此

所以当时,
x-y取最小值.

知识点

函数的值域利用基本不等式求最值

题型：单选题

单选题 · 5 分

6.已知a=(x,1),b=(2,-x),那么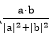的取值范围是（　　）

正确答案

解析

若x=0,

则

若x>0,由于

则

若x<0,由于

则

那么

即-

知识点

平面向量数量积的运算利用基本不等式求最值

继续学习学习下一知识点

下一知识点 : 不等式与函数的综合问题

百度题库 > 高考 > 理科数学 > 利用基本不等式求最值

扫码查看完整答案与解析