- 命题及其关系、充分条件与必要条件
- 共1031题
5.设集合M＝{x|0<x≤3}，N＝{x|0<x≤2}，那么“a∈M”是“a∈N”的( )
正确答案
解析
略。
知识点
5.设函数f(x)＝cos(2x＋φ)，则“f(x)为奇函数”是“φ＝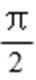
正确答案
必要不充分
解析
略。
知识点
1.设
正确答案
解析
略
知识点
22.已知函数f（x）=ax+
（1）若f（x）≥lnx在[1，+∞）上恒成立，求a的取值范围；
（2）证明：1+
（3）已知S=1+
正确答案
见解析。
解析
（1）∵函数f（x）=ax+
f（x）≥lnx在[1，+∞）上恒成立，
设g（x）=f（x）﹣lnx，则g（x）=f（x）﹣lnx≥0在[1，+∞）上恒成立，
∴g（x）min≥0，
又∵g′（x）=a﹣
而当
①当
g′（x）≥0在[1，+∞）上恒成立，
∴g（x）min=g（1）=0≥0；
②当
g′（x）=0时x=
且1≤x＜
当x＞
则g（x）min=g（
又∵g（
∴综上所述，a的取值范围为：[
（2）证明：由（1）可知a
则当a=
令x依次取
则有 
… 
由同向不等式可加性可得
即 
也即 
也即1+
（3）由（2）的结论，可得，S=1+
又S=1+
则有S的整数部分为9。
知识点
3.在
正确答案
解析
因为
知识点
6.若命题“∃x0∈R，x＋(a－1)x0＋1＜0”是真命题，则实数a的取值范围是( )
正确答案
解析
因为命题“∃x0∈R，x＋(a－1)x0＋1＜0”等价于x＋(a－1)x0＋1＝0有两个不等的实根，所以Δ＝(a－1)2－4＞0，即a2－2a－3＞0，解得a＜－1或a＞3，故选D.
知识点
9.下面命题中假命题是（ ）
A∀x∈R，3x＞0
B∃α，β∈R，使sin（α+β）=sinα+sinβ
C∃m∈R，使
D命题“∃x∈R，x2+1＞3x”的否定是“∀x∈R，x2+1＞3x”
正确答案
解析
A，根据指数函数的性质可知，∀x∈R，3x＞0，∴A正确．
B，当α=β=0时，满足sin（α+β）=sinα+sinβ=0，∴B正确．
C，当m=1时，幂函数为f（x）=x3，且在（0，+∞）上单调递增，∴C正确．
D，命题“∃x∈R，x2+1＞3x”的否定是“∀x∈R，x2+1≤3x”，∴D错误．
故选：D.
知识点
5.①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②若两个随机变量的线性相关性越强，则相关系数的绝对值越接近于1；
③根据散点图求得的回归直线方程可能是没有意义的；
④若某项测量结果ξ服从正态分布N（1，σ2），且P（ξ≤4）=0.9，则P（ξ≤﹣2）=0.1。
其中真命题的个数为（ ）
正确答案
解析
略。
知识点
8.下面命题中假命题是（ ）
A∀x∈R，3x＞0
B∃α，β∈R，使sin（α+β）=sinα+sinβ
C∃m∈R，使
D命题“∃x∈R，x2+1＞3x”的否定是“∀x∈R，x2+1＞3x”
正确答案
解析
A根据指数函数的性质可知，∀x∈R，3x＞0，∴A正确．
B当α=β=0时，满足sin（α+β）=sinα+sinβ=0，∴B正确．
C当m=1时，幂函数为f（x）=x3，且在（0，+∞）上单调递增，∴C正确．
D命题“∃x∈R，x2+1＞3x”的否定是“∀x∈R，x2+1≤3x”，∴D错误．
故选：D.
知识点
16．已知
①
② 直线
③ 函数
④ 函数
其中所有正确命题的序号为_________。
正确答案
①②④
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析