- 命题及其关系、充分条件与必要条件
- 共1031题
14.设




正确答案
解析
由题可知,易得由x=1且y=2可推出x+y=3,反之不成立。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查简易逻辑
解题思路
本题直接判断,即可得到结果。
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在前后互推判断时发生错误。
知识点
16.设


正确答案
解析
(1)若
当

即“


(2)若
当

即“


综上所述,“

考查方向
本题考查充分条件、必要条件、充分必要条件的判断以及不等式的性质,是容易题,涉及充分必要条件的问题在近几年的各省高考题中出现的频率非常高,它可以与高中数学每一个章节每一个知识点相结合进行命题,是高考的热点问题.
解题思路
根据不等式的性质,先判断“





易错点
对充分性和必要性的认识不足,混淆不等式的各种性质以及各性质需要的前提条件.
知识点
6.设


正确答案
解析
因为





考查方向
解题思路
1、充分条件的判断可以通过取特殊值进行验证;
2、必要条件的判断可以通过不等式的基本性质进行判断。
易错点
1、本题易在不理解充分条件与必要条件的含义而导致错误。
2、本题在应用不等式的性质时会因为疏忽符号而出现错误。
知识点
6.设


正确答案
解析
由





考查方向
解题思路
先由

易错点
解不等式容易出错。
知识点
15.设




正确答案
解析
知识点
4.设


正确答案
解析



所以
考查方向
解题思路
由基本运算入手
易错点
考虑过多,想到向量的零向量,以及向量平行的同向和反向两种情况而误导出错
知识点
5.设


正确答案
解析
因为函数

所以


应选C.
考查方向
解题思路
1.构造函数;
2.由函数的单调性和充要条件的定义加以解决。应选C。
易错点
本题想不到用构造函数的方法解决,找不到函数模型。
知识点
3. “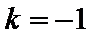
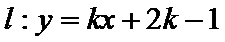
正确答案
解析
把直线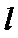
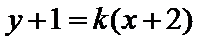
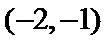
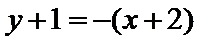
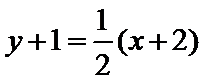
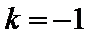
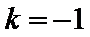
考查方向
解题思路
根据题意将直线化为点斜式方程,结合图象进行分析;
易错点
1、本题易在不理解充分条件与必要条件的含义而导致错误。
2、本题容易忽略直线在坐标轴上的截距为0而错选B。
知识点
16.下列说法中所有正确的序号是________
①、
②、若
③、
④、数列
正确答案
①③④
解析
对于①,

对于②,



对于③,由题意知




对于④,








考查方向
解题思路
逐个判断真假即可。
易错点
1. ②中很容易选错,③感觉无从下手;
2.对于④的单调性不能很好的利用对勾函数的单调性导致无法判断。
知识点
7.定义在






正确答案
解析
由






因为对任意的


















若





















考查方向
解题思路
本题属于中等题,可使用数形结合法,
(1)由

(2)由




(3)利用图形可得结论。
易错点
不会利用已知条件求函数的对称轴,不会判断函数的单调性,搞不清充分条件与必要条件。
知识点
扫码查看完整答案与解析









