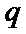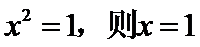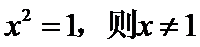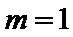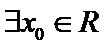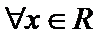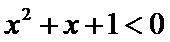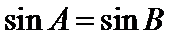- 命题及其关系、充分条件与必要条件
- 共1031题
3.设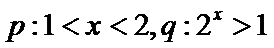


正确答案
解析
由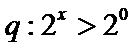
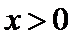
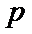
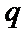
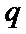
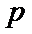

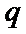
考查方向
解题思路
先利用指数函数的运算法则,然后判断是什么样的条件。
易错点
充分条件和必要条件混淆
知识点
3.实数a=3是直线ax+2y+3a=0和直线3x+(a-1)y=a-7平行的( )
正确答案
解析
若直线ax+2y+3a=0和直线3x+(a-1)y=a-7平行,则有
考查方向
解题思路
先求出两直线平行时的充要条件(a=3),再判断a=3是该条件成立的什么条件。
因此A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
易忽视两直线重合的情况
知识点
3.下列选项错误的是()
正确答案
解析
1、原命题与逆否命题的关系确定A正确
2、根据充分必要条件的判定确定B正确
3、根据全(特)称命题的否定确定C正确
4、最后选择D
考查方向
解题思路
1、原命题与逆否命题的关系确定A正确
2、根据充分必要条件的判定确定B正确
3、根据全(特)称命题的否定确定C正确
4、最后选择D
易错点
本题易错于全(特)称命题的否定理解不足,导致无法排除
知识点
3.在


正确答案
解析
∵在

∴

∴所以选项A为正确选项
考查方向
解题思路
在

易错点
本题易在充分必要条件的判定混淆使用
知识点
4.“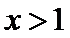
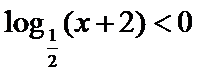
正确答案
解析
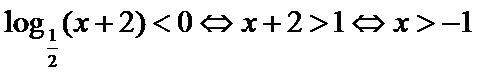
考查方向
解题思路
用集合的观点看充分条件、必要条件:A={x|x满足条件p},B={x|x满足条件q},(1)如果A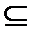
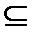
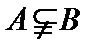
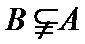
易错点
本题易错点在于解对数不等式时没有考虑对数的定义域.
知识点
8.设a,b都是不等于1的正数,则“
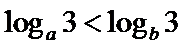
正确答案
解析
若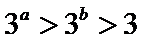
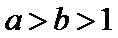
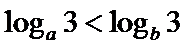
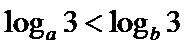
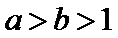
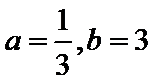
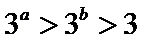
考查方向
解题思路
直接根据充要条件的判断方法判断即可。
易错点
对于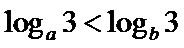
知识点
5.已知命题







正确答案
解析




考查方向
解题思路
分别判断命题p,q的真假, 再分析复合命题的真假
易错点
复合命题的真值判断易出错
知识点
4.“C=5”是“点(2,1)到直线3x+4y十C=0的距离为3”的( )
正确答案
解析
由题意知点







考查方向
解题思路
先求出点(2,1)到直线3x+4y十C=0的距离为3的充要条件的C的值为

易错点
采用代入验证出错。
知识点
3.下列有关命题的说法正确的是
正确答案
解析
命题“若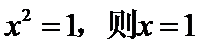
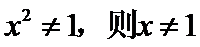

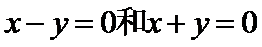
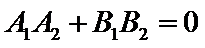
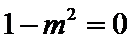

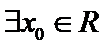
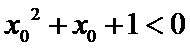
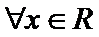
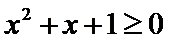
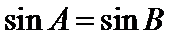
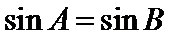
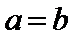
考查方向
解题思路
1)否命题的定义是否定题设和结论;
2)两直线垂直的充要条件是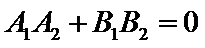
3)特称命题的否定是将特称改为全称,否定结论;
4)逆命题是题设和结论互换,然后判断若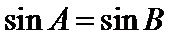
易错点
本题易在判定命题的否定和否命题时出现错误,以及判断必要条件时出现错误,两直线垂直的充要条件用错,三角形中角和正弦值之间的关系也易错。
知识点
1.设


正确答案
解析
若“



考查方向
解题思路
结合不等式的性质,按照充分条件与必要条件的关系直接推导.
易错点
应用不等式的性质易忽略条件.
知识点
扫码查看完整答案与解析