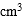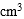- 命题及其关系、充分条件与必要条件
- 共1031题
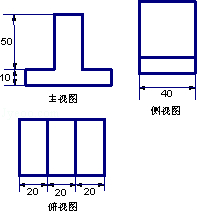
一简单组合体的三视图及尺寸如图（1）示（单位：cm）则该组合体的体积为，（ ）
A72000
B64000
C56000
D44000
正确答案
解析
由三视图知，该组合体由两个直棱柱组合而成，上部长方体三度为：40，20，50；
下部长方体三度为：60，40，10；
故组合体的体积V=60×40×10+20×40×50=64000（cm3），
故选B。
知识点
“
正确答案
解析
由
知识点
现有如下命题：
①过平面外一点有且只有一条直线与该平面垂直；
②过平面外一点有且只有一条直线与该平面平行；
③如果两个平行平面和第三个平面相交，那么所得的两条交线平行；
④如果两个平面相互垂直，那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内。
则所有真命题的序号是 。
正确答案
①③④
解析
①过平面外一点有且只有一条直线与该平面垂直，正确；
②过平面外一点有且只有一条直线与该平面平行，错误，应该是有无数条直线与该平面平行；
③如果两个平行平面和第三个平面相交，那么所得的两条交线平行，正确，由平面与平面平行的性质定理可得；
④如果两个平面相互垂直，那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内，正确，
由平面与平面垂直的性质定理可得。
故答案为：①③④
知识点
已知直线
正确答案
解析
当
知识点
在四边形ABCD中，“
正确答案
解析
由
由
∴对角线互相垂直的平行四边形是菱形。
反之也成立。
∴“
故选C。
知识点
“
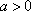
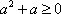
正确答案
解析
因为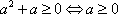
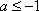
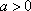
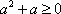
但“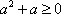
知识点
已知命题
正确答案
解析
知识点
“p且q是真命题”是“非p为假命题”的( )
正确答案
解析
p且q是真命题，则p、q一定是真命题，从而非p是假命题，因此充分性成立；当非p是假命题时，p一定是真命题，但p有可能是假命题，则p且q就是假命题，所以，必要性不成立，选A。
知识点
设
正确答案
解析
令
知识点
若p是q的必要条件，s是q的充分条件，那么下列推理一定正确的是
A
B
C
D
正确答案
解析
因为p是q的必要条件，s是q的充分条件
所以q⇒p，s⇒q，
所以s⇒p,
所以
故选：C
知识点
扫码查看完整答案与解析