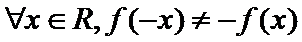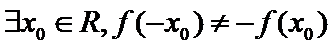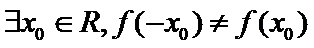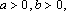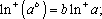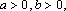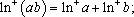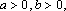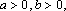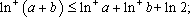- 命题及其关系、充分条件与必要条件
- 共1031题
4．设
正确答案
解析
考查方向
解题思路
直接按充分条件与必要条件的方法去判断。
易错点
判断失误。
知识点
3.下列选项错误的是（）
A命题 “若
B“
C若命题“
D若“
正确答案
解析
1、原命题与逆否命题的关系确定A正确
2、根据充分必要条件的判定确定B正确
3、根据全（特）称命题的否定确定C正确
4、最后选择D
考查方向
解题思路
1、原命题与逆否命题的关系确定A正确
2、根据充分必要条件的判定确定B正确
3、根据全（特）称命题的否定确定C正确
4、最后选择D
易错点
本题易错于全（特）称命题的否定理解不足，导致无法排除
知识点
3.设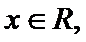
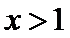
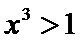
正确答案
解析
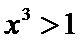
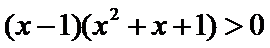
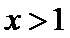
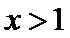
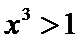
考查方向
解题思路
先解不等式得到前后范围相同，后即可得到答案。
易错点
不会解不等式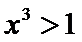
知识点
5．已知命题
A
B
C
D
正确答案
解析
考查方向
解题思路
分别判断命题p,q的真假, 再分析复合命题的真假
易错点
复合命题的真值判断易出错
知识点
2．若直线
正确答案
解析
由向量共线的定义可知，两直线平行可以得到
考查方向
解题思路
分别判断。
易错点
判断出错。
知识点
13．若
正确答案
解析
由判别式小于等于0，即实数
考查方向
解题思路
直接由判别式小于等于0即可。
易错点
不会转化。
知识点
3.设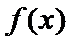
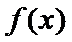
A
B
C
D
正确答案
考查方向
解题思路
1.先根据奇函数的定义得到题中命题的逆否命题；
易错点
1.全称命题的否定形式写错；2.不能正确理解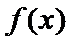
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
下列命题中，假命题为( )
A存在四边相等的四边形不是正方形
Bz1，z2∈
C若x，y∈
D对于任意n∈
正确答案
解析
A项中，四边相等的空间四边形显然不是正方形，故A项为真命题；B项中，z1，z2∈C，“z1＋z2为实数”⇐“z1，z2互为共轭复数”，但“z1＋z2为实数”D
知识点
定义“正对数”: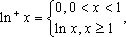 
①若
②若
③若
④若
其中真命题有____________.（写出所有真命题的编号）
正确答案
①③④
解析
略。
知识点
扫码查看完整答案与解析