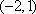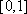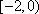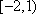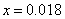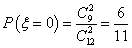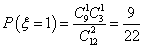- 直线和圆的方程的应用
- 共43题
“

正确答案
解析
略
知识点
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动。当圆滚动到圆心位于(2,1)时,
正确答案
解析
根据题意可知圆滚动了2单位个弧长,点P旋转了


知识点
某写字楼将排成一排的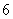
正确答案
24
解析
略
知识点
已知函数
(1)讨论
(2)若对于任意的a∈[1,2],函数
正确答案
见解析。
解析
(1)

(2)


知识点
对任意实数
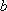
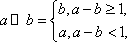
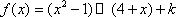
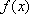

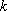
正确答案
解析
略
知识点
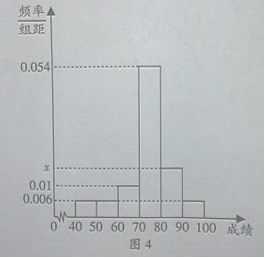
某班50位学生期中考试数学成绩的频率分布直方图如图4所示,其中成绩分组区间是:
[40,50), [50,60), [60,70), [70,80), [80,90), [90,100],
(1)求图中x的值;
(2)从成绩不低于80分的学生中随机选取2人,2人中成绩在90分以上(含90分)的人数记为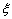
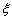
正确答案
见解析。
解析
(1)由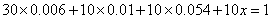
(2)由题意知道:不低于80分的学生有12人,90分以上的学生有3人
随机变量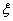
∴
知识点
某车间共有

(1) 根据茎叶图计算样本均值;
(2) 日加工零件个数大于样本均值的工人为优秀工人.
根据茎叶图推断该车间
(3) 从该车间


正确答案
(1)22;(2)4;(3) 
解析
(1) 样本均值为
(2) 由(1)知样本中优秀工人占的比例为


(3) 设事件




知识点
已知

正确答案
解析
设

则
知识点
已知i为虚数单位,则复数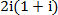
正确答案
解析
略
知识点
某地一渔场的水质受到了污染,渔场的工作人员对水质检测后,决定往水中投放一种药剂来净化水质. 已知每投放质量为

(1)如果投放的药剂质量为m=6,试问渔场的水质达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在8天(从投放药剂算起包括第8天)之内的渔场的水质达到最佳净化,试确定应该投放的药剂质量m的取值范围。
正确答案
(1)8天;
(2)[6,9]
解析
(1)由已知得,经过x天该药剂在水中释放的浓度 y=mf(x)是关于自变量





(1)由题设:投放的药剂质量为





所以如果投放的药剂质量为
(2)由题设:


∴

∴



知识点
扫码查看完整答案与解析