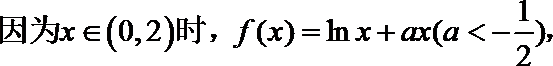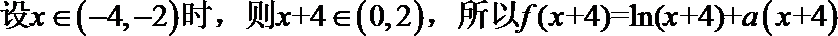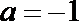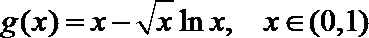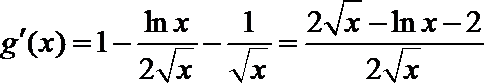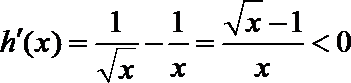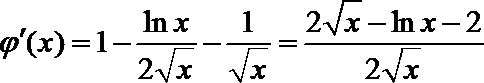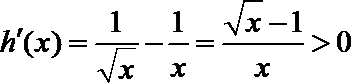- 直线和圆的方程的应用
- 共43题
在平面几何中有如下结论：若正三角形ABC的内切圆面积为
正确答案
解析
内切球半径与外接球半径之比为
知识点
已知a>0且
正确答案
解析
∵
∴
由（1）得
由（2）得
∴原不等式的解集是
知识点
如图，C是以AB为直径的半圆O上的一点，过C的直线交，直线AB于E，交过A点的切线于D，BC∥OD 。
（1）求证：DE是圆O的切线；
（2）如果AD =AB = 2，求EB 。
正确答案
见解析
解析
（1）证：连接AC，AB是直径，则BC⊥AC
由BC∥OD ⇒OD⊥AC
则OD是AC的中垂线⇒ ∠OCA =∠OAC , ∠DCA =∠DAC ,
⇒ ∠OCD = ∠OCA +∠DCA =∠OAC +∠DAC =∠DAO = 90o 。
⇒OC⊥DE, 所以DE是圆O的切线 。
（2）BC∥OD⇒∠CBA = ∠DOA，∠BCA = ∠DAO ⇒△ABC∽△AOD
⇒ 
⇒ BE =
知识点
15.已知AB是半圆O的直径，点C在半圆上，CD⊥AB于点D，且AD=4DB，设∠COD=θ，则cos2θ=________。
正确答案
-
解析
略。
知识点
6.设
A若
B若
C若
D若
正确答案
解析
若
知识点
17. 甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为
（Ⅰ）求甲乙二人中至少有一人破译出密码的概率；
（Ⅱ）求
（Ⅲ）设甲、乙、丙三人中破译出密码的人数为
正确答案
解：记“甲、乙、丙三人各自破译出密码”分别为事件
依题意有
（Ⅰ）甲、乙二人中至少有一人破译出密码的概率为
（Ⅱ）设“三人中只有甲破译出密码”为事件
所以
（Ⅲ）
所以
所以，
解析
解析已在路上飞奔，马上就到！
知识点
17．已知函数
A
B
C
D（0，0）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21.已知函数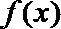
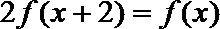
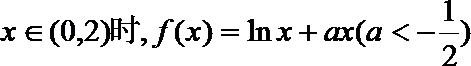
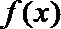
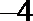
（Ⅰ）求
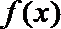
（Ⅱ）是否存在实数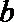
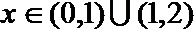
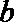
正确答案
（1）由已知得：
∴
∴
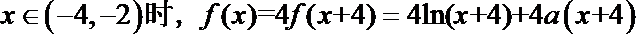
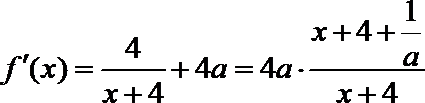
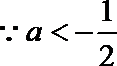
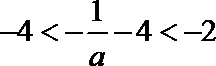
∴当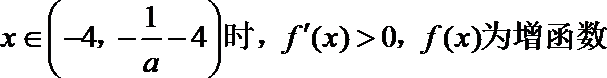
当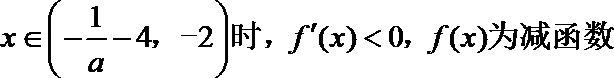
∴
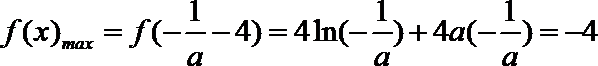
∴当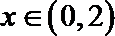
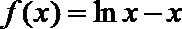
（2）由（1）可得：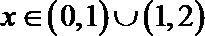
即为
①当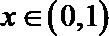
则
令
∴
∴
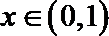
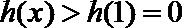
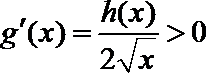
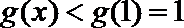
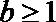
②当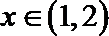
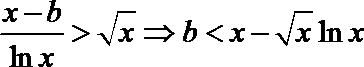
则
令
∴
∴
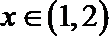
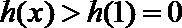
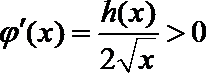
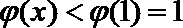
综上所述：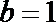
解析
解析已在路上飞奔，马上就到！
知识点
20.向量
（1）求数列
（2）求
（3）记
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．曲线
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析