- 函数零点的判断和求解
- 共205题
21.己知函数f(x)=a(x-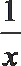
(1)若f(x)有极值,求a的取值范围;
(2)讨论(x)的零点个数,并说明理由.(参考数值:ln2≈0. 6931)
正确答案
(1)0<a<1;
(2)当a≤0或a≥1时,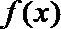
解析
本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求;
(2)要注意对参数的讨论.
(1)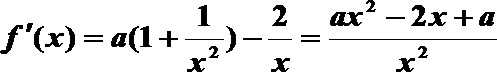
因为f(x)定义域为(0,+∞),
所以ax2-2x+a=0有正根且不为等根。
显然a≠0,由x1x2=1>0.得Δ>0且x1+x2>0,所以 0<a<1 。
(2)由上知,
因为x∈(0,+∞),①若a≤0,则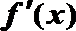
②若a≥1,则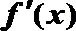
③若0<a<1,记x1,x2分别为ax2-2x+a=0的两根,且x1<1<x2,且f(x)在(0,x1)单调递增,在(x1,x2)单调递增,(x2,+∞)单调递增。
因为f(1)=0,所以f(x1)>0,f(x2)<0.当x∈(0,x1)时,取
显然,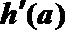
所以h(a)在(0,1)单调递增,所以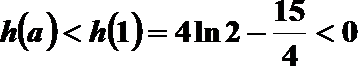
故
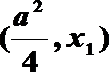
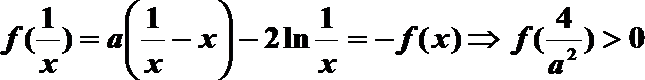
则f(x)在
综上可知:当a≤0或a≥1时,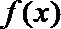
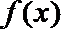
考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
无
易错点
第二问中的易丢对a的分类讨论。
知识点
12.函数

正确答案
解析
首先构造两个函数


(1)当

(2)当

(3)当



考查方向
解题思路
首先构造两个函数


易错点
1、忽略对数函数的定义域导致结果出错
2、没有注意到后面的二次函数过原点,而增加不必要的讨论和计算
知识点
8.定义在R上的奇函数




正确答案
解析
通过图象大致情况,可以求出零点,并可以判断出零点的和为
考查方向
解题思路
先根据奇函数的性质求f(x)图像,利用数列求和
易错点
根据零点的位置 推导出规律求零点的和
知识点
12.若函数f(x)=x3+ax2+bx+c有极值点x1,x2,且f(x1)=x1<x2,则关于x的方程

正确答案
解析




考查方向
解题思路
本题考查了函数零点的概念以及对嵌套型函数的理解,涉及到函数的零点个数问题通常优先考虑数形结合的方法来解决,
本题中,对函数




易错点
本题易在应用数形结合的过程中出现错误。
知识点
16.已知函数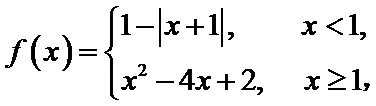

正确答案
2
解析
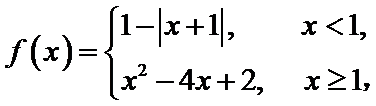
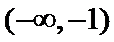
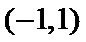
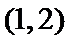
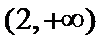
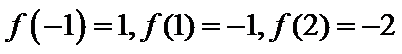
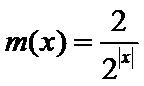
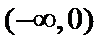
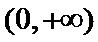
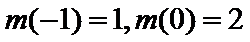

考查方向
本题考查了函数的零点个数问题,但可转化为两个函数图像的交点个数问题,体现了数形结合的思想。
解题思路
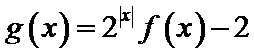
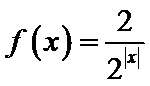
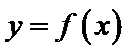
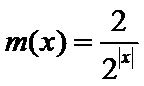
易错点
函数向方程的转化不得当,会造成函数图像画不好,影响解题。
知识点
12.函数

正确答案
解析
当

当





故方程

应选D.
考查方向
解题思路
1.由
2.由
易错点
1找不到分类讨论的突破口,即分类的标准;
2.不能把零点问题转化为方程的解进行解决。
知识点
12.已知




正确答案
解析
令
























考查方向
解题思路
1.先求出
2.根据 




易错点
1.无法做出
2. 满足

知识点
8.已知




正确答案
解析
由题可知:f(x)≥2m,且f(0)=6m. 若函数


A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
代入特值计算或由函数的基本性质,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在代特值时发生错误。
知识点
9. 若定义在R上的函数f(x)满足f(-x)=f(x), f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)= |xex|-f(x)在区间
正确答案
解析
f(-x)=f(x), f(2-x)=f(x),所以f(x)是偶函数、周期是2
令
求导得,





根据



考查方向
解题思路
先看懂这个四分之一圆所表示的图像只是函数的一部分构成的,然后根据函数的奇偶性以及周期性即可得到在区间[-3,1]上的f(x)图象。
易错点
看不懂图所表示的四分之一圆导致不知道从什么地方入手,对函数奇偶性周期性不熟悉导致出错,在计算函数的单调性时,不清楚函数的零点定义也会出错。再者就是计算出错。
知识点
15.已知函数

正确答案
解析
考查方向
解题思路
该题信息量比较大关键在于理清解题思路
易错点
本题易错点有:1、图像画不出,2、关于
知识点
扫码查看完整答案与解析





























