- 函数零点的判断和求解
- 共205题
16.已知函数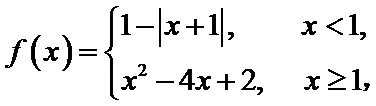

正确答案
2
解析
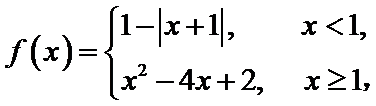
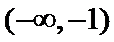
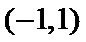
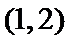
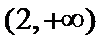
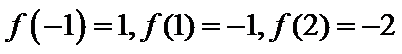
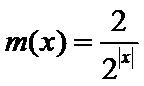
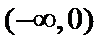
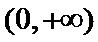
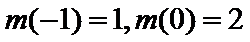

考查方向
本题考查了函数的零点个数问题,但可转化为两个函数图像的交点个数问题,体现了数形结合的思想。
解题思路
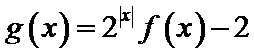
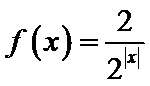
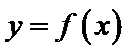
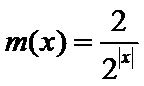
易错点
函数向方程的转化不得当,会造成函数图像画不好,影响解题。
知识点
12.已知




正确答案
解析
令
























考查方向
解题思路
1.先求出
2.根据 




易错点
1.无法做出
2. 满足

知识点
8.已知




正确答案
解析
由题可知:f(x)≥2m,且f(0)=6m. 若函数


A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
代入特值计算或由函数的基本性质,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在代特值时发生错误。
知识点
9. 若定义在R上的函数f(x)满足f(-x)=f(x), f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)= |xex|-f(x)在区间
正确答案
解析
f(-x)=f(x), f(2-x)=f(x),所以f(x)是偶函数、周期是2
令
求导得,





根据



考查方向
解题思路
先看懂这个四分之一圆所表示的图像只是函数的一部分构成的,然后根据函数的奇偶性以及周期性即可得到在区间[-3,1]上的f(x)图象。
易错点
看不懂图所表示的四分之一圆导致不知道从什么地方入手,对函数奇偶性周期性不熟悉导致出错,在计算函数的单调性时,不清楚函数的零点定义也会出错。再者就是计算出错。
知识点
15.已知函数

正确答案
解析
考查方向
解题思路
该题信息量比较大关键在于理清解题思路
易错点
本题易错点有:1、图像画不出,2、关于
知识点
扫码查看完整答案与解析













