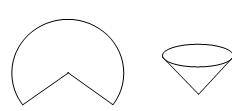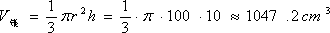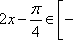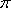- 空间几何体的结构特征
- 共964题
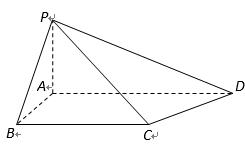
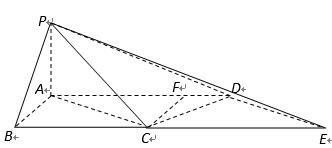
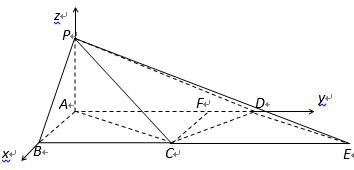
如图,在四棱锥









(1)求证:

(2)若点




正确答案
见解析
解析
解法一:取




则









(2)设

设平面
令

设两个法向量的夹角为




解法二:(1)因为底面


又







(2)因为点


所以

过



因为



因为
在


知识点
如图,用半径为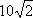
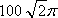
正确答案
见解析
解析
设铁皮扇形的半径和弧长分别为R、l,圆锥形容器的高和底面半径分别为h、r,则由题意得R=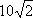
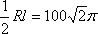
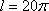
由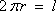
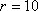
由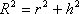
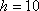
由
所以该容器最多盛水1047.2cm3 ………………………12分
(说明: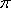
知识点
已知向量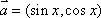
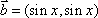
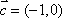
(1)若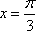
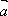
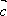
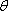
(2)若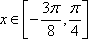
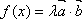

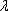
正确答案
见解析
解析
(1)当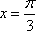
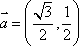
所以 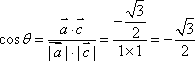
因而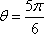
(2)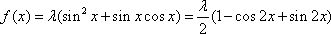
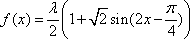
因为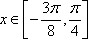
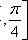
当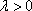
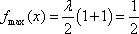
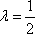
当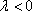
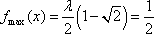
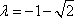
所以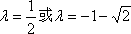
知识点
已知向量


(1)求函数
(2)记△





正确答案
见解析
解析
(1)

所以
递减区间是
(2)由


当




当




知识点
在四边形




(1)求
(2)求四边形
正确答案
见解析。
解析
(1)
如图,连结

在
在
由
从而
(2)由(1)可知
所以
知识点
已知长方体的一个顶点上的三条棱长分别是
正确答案
解析
因为球的半径为R=

为
知识点
已知向量



且

(1)求

(2)若


正确答案
见解析。
解析
(1)

∴





(2)由(1)可得
∵ 


∴当


当

∴

知识点
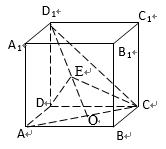
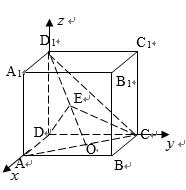
如图:在正方体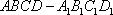

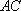
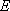
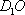
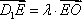
(1)求证: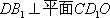
(2)若平面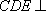
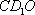
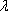
正确答案
见解析
解析
(1)不妨设正方体的棱长为1,如图建立空间直角坐标系,
则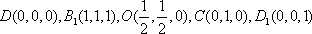
于是: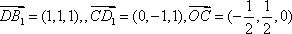
因为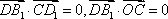
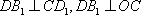
故: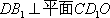
(2)由(1)可知平面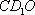
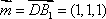
由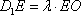
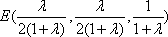
又设平面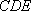
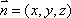
得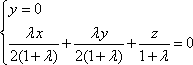
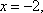
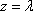
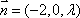
因为平面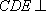
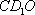
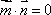
知识点
如图,在四棱锥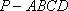
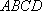
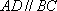
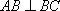
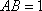
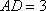
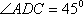
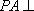
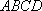
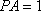
(1)异面直线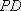
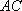
(2)四棱锥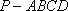
正确答案
见解析
解析
(1)连接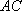
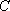
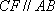
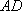
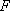
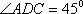
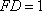
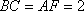
解法1:延长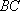
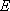
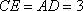
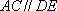
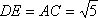
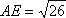
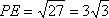
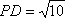
在△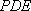
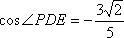
所以,异面直线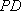
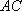
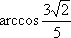
解法2:建立如图所示的空间直角坐标系.
则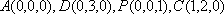
所以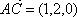
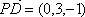
设异面直线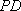
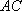
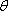
则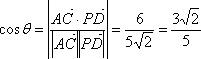
所以异面直线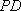
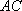
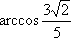
(2)底面梯形面积为

所以,四棱锥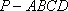
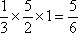
知识点
正三棱柱



(1)求侧棱
(2)求二面角
正确答案
见解析。
解析
(1)取





(2)过





连接

余弦值为
知识点
扫码查看完整答案与解析