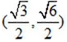- 正弦定理
- 共176题
21. ABC中,a、b、c分别是角A、B、C的对边,


(1)判断△ABC的形状;
(2)若

正确答案
(1)
⇒sinBsinA﹣sinBsin2C=sinAsin2C﹣sinBsin2C
⇒sinB=sin2C,
因为
所以B=π﹣2C⇒B+C=π﹣C⇒π﹣A=π﹣C⇒A=C
即△ABC为等腰三角形.
(2)因为
所以
而
所以
解析
解析已在路上飞奔,马上就到!
知识点
15.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在
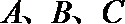
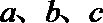
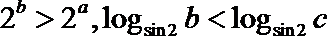
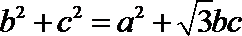
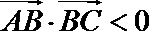
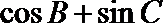
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在


(1)求角B的大小;
(2)设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在



(1)求角B的大小;
(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
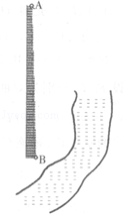
17.要测量河对岸的烟囱AB,而测量者又不能到达它的底部,现有测角仪和钢卷尺两种测量工具,请你设计一种测量方案.要求
(I)画出图形,指出要测量的数据(用字母表示并在图中标出);
(II)用文字和公式写出计算烟囱高AB的步骤(测角仪的高度忽略不计)
正确答案
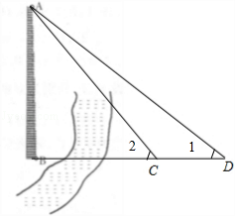
要测量河对岸的烟囱AB;如图:
(Ⅰ)在C出测得对烟囱AB的仰角∠2后退m米,在D处测得对烟囱AB的仰角∠1.
(Ⅱ)需要工具有测角仪与米尺.
在C出测得对烟囱AB的仰角∠2后退m米,在D处测得对烟囱AB的仰角∠1.
利用直角三角形列出关系式即可求出AB.

所以BC=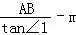

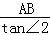
所以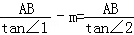
解得
AB=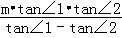
解析
解析已在路上飞奔,马上就到!
知识点
17.在
(I)求
(II)设AC=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 在锐角


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知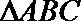
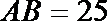

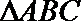


(1)若外接圆O的半径为
(2)求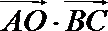
正确答案
(1)由正弦定理有
∴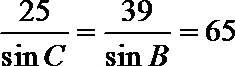
∴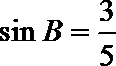
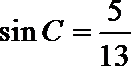
且B为钝角,
∴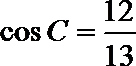
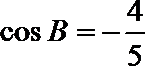
∴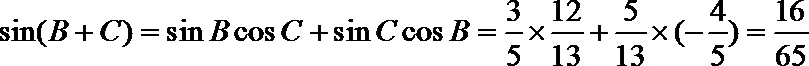
又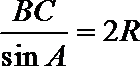
∴
(2)由已知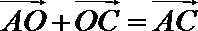
∴
即
同理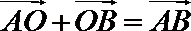
∴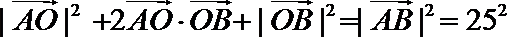
两式相减得
即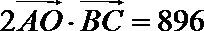
∴
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析