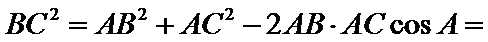正弦定理_章节学习

1

题型：单选题

|

单选题 · 5 分

已知△ABC是边长为1的等边三角形，点D、E分别是边AB、BC的中点，连接DE并延长到点F，使得DE=2EF，则的值为

A

B

C

D

正确答案

B

知识点

正弦定理

1

题型：简答题

|

简答题 · 12 分

在△ABC中，角A,B,C所对的边分别是a,b,c,且.

19.证明：；

20.若，求.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）根据正弦定理，可设===k(k>0)．

则a=ksin A，b=ksin B，c=ksin C．

代入+=中，有

+=，变形可得

sin Asin B=sin Acos B+cos Asin B=sin(A+B)．

在△ABC中，由A+B+C=π，有sin(A+B)=sin(π–C)=sin C，

所以sin Asin B=sin C．

解析

（I）证明：由正弦定理可知原式可以化解为

∵和为三角形内角 , ∴则，两边同时乘以，可得由和角公式可知，原式得证。

考查方向

本题主要考查了正弦定理、余弦定理、商数关系、平方关系.考查学生的分析问题的能力和计算能力

解题思路

本题考查正弦定理、余弦定理、商数关系等基础知识，考查学生的分析问题的能力和计算能力.在解三角形的应用中，凡是遇到等式中有边又有角时，可用正弦定理进行边角互化，一种是化为三角函数问题，一般是化为代数式变形问题．在角的变化过程中注意三角形的内角和为这个结论，否则难以得出结论．

易错点

本题考查正弦定理、余弦定理、商数关系等基础知识，在用化边为角的技巧应用中有时会发生错误。

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）4.

解析

（II）由题,根据余弦定理可知，

∵为为三角形内角，，

则，即由（I）可知，∴ ∴

考查方向

本题主要考查了正弦定理、余弦定理、商数关系、平方关系.考查学生的分析问题的能力和计算能力

解题思路

本题考查正弦定理、余弦定理、商数关系等基础知识，考查学生的分析问题的能力和计算能力.在解三角形的应用中，凡是遇到等式中有边又有角时，可用正弦定理进行边角互化，一种是化为三角函数问题，一般是化为代数式变形问题．在角的变化过程中注意三角形的内角和为这个结论，否则难以得出结论．

易错点

本题考查正弦定理、余弦定理、商数关系等基础知识，在用化边为角的技巧应用中有时会发生错误。

1

题型：填空题

|

填空题 · 5 分

13．在中，内角所对的边分别为，已知的面积为，则的值为 .

正确答案

8

解析

因为，所以，

又，解方程组得，由余弦定理得

，所以.

考查方向

1.同角三角函数关系；2.三角形面积公式；3.余弦定理.

解题思路

根据1.同角三角函数关系；2.三角形面积公式；3.余弦定理.结合已知条件构造方程组解出即可。

易错点

定理不熟悉。

知识点

正弦定理余弦定理三角形中的几何计算

1

题型：填空题

|

填空题 · 4 分

12．若锐角的面积为，且，则等于________．

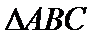
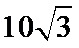
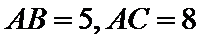
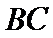
正确答案

解析

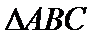
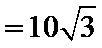
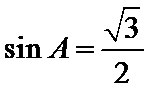
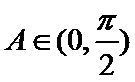
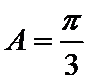
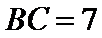
由已知得的面积为，所以，，所以．由余弦定理得，．

考查方向

1、三角形面积公式；2、余弦定理．

解题思路

利用三角形的面积公式求出A，再利用余弦定理求出BC.

易错点

计算能力弱，不会用余弦定理求三角形的面积

知识点

正弦定理余弦定理三角形中的几何计算

1

题型：填空题

|

填空题 · 5 分

16．在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是 .

正确答案

（，）.

解析

如图所示，延长BA，CD交于E，平移AD，当A与D重合与E点时，AB最长，在△BCE中，∠B=∠C=75°，∠E=30°，BC=2，由正弦定理可得，即，解得=，平移AD ，当D与C重合时，AB最短，此时与AB交于F，在△BCF中，∠B=∠BFC=75°，∠FCB=30°，由正弦定理知，，即，解得BF=，所以AB的取值范围为（，）.

考查方向

正余弦定理；数形结合思想

解题思路

本题可对边进行延长，由正弦定理求出BE然后求出BF,即可得到AB的范围。

易错点

本题在综合应用正余弦定理时易错。

知识点

正弦定理余弦定理三角形中的几何计算

1

题型：简答题

|

简答题 · 12 分

设△ABC的内角A,B,C的对边分别为，.

18.证明：;

19.若 ,且B为钝角，求A,B,C.

第(1)小题正确答案及相关解析

正确答案

由及正弦定理得，所以。

解析

见答案

考查方向

本题主要考察正弦定理及其应用，意在考察考生的运算求解能力和转化能力。

解题思路

由题及正弦定理得可得。

易错点

不会想到切割化弦；

第(2)小题正确答案及相关解析

正确答案

,,.

解析

因为，所以，

由（1）知，因此，又B为钝角，所以，

故，由知，从而，

综上所述，,,.

考查方向

本题主要考察正弦定理及其应用，意在考察考生的运算求解能力和转化能力。

解题思路

由两角和与差的公式化简得，结合（1）得，又B为钝角，所以求出角，进而可以求出角A,C。

易错点

做第（2）问时联系不上第（1）问的结论。

1

题型：简答题

|

简答题 · 14 分

15．在中，，

（1）求的值；

（2）若点D在边上，，求的长。

正确答案

见解析

解析

解：如图，设的内角所对边的长分别是，由余弦定理得，所以.

又由正弦定理得.

由题设知，所以.

在中，由正弦定理得.

考查方向

本题考查了利用正余弦定理，求三角函数值及边长

解题思路

（1）用余弦定理求a

（2）由正弦定理求sinB

（3）在，由正弦定理求AD

易错点

忽略数形结合思想在本题中的作用。

知识点

同角三角函数间的基本关系正弦定理解三角形的实际应用

1

题型：填空题

|

填空题 · 5 分

13. 在ABC中，角A，B，C所对的边分别为a，b，c. 若，，，则____；ABC的面积为____.

正确答案

解析

由＝sinB得Ａ＝Ｂ，即a=b=3,从而由余弦定理得，从而得，由面积公式得：ABC的面积为.

考查方向

本题主要考查三角函数的诱导公式及余弦定理和面积公式的相关知识，为高考历年必考题。

解题思路

由＝sinB,进而得出Ａ＝Ｂ，即a=b=3,从而由余弦定理得出cosC的值，然后根据三角函数基本关系式得出sinC的值运用面积公式可求ABC的面积。

易错点

考查知识点相对较多，基础不扎实，对个别公式掌握不熟练而出错。

知识点

诱导公式的作用正弦定理

1

题型：单选题

|

单选题 · 5 分

7.在△ ABC中，a，b, c分别是角A，B，C所对边的边长，若cos A + sin A- =0,则的值是（）

A1

B

C

D2

正确答案

B

解析

得∴,∴利用正弦定理知

考查方向

本题主要考查解三角形

解题思路

利用两角和与差的正弦、余弦函数公式化简，根据正弦、余弦函数求出cos(A+B)与sin(A+B)的值，进而求出A,B,C的度数，利用正弦定理化简所求的式子，计算即可得到结果

易错点

利用正余弦定理边角互化

知识点

正弦定理解三角形的实际应用

1

题型：单选题

|

单选题 · 5 分

在中，角A，B，C的对边分别为若，则角B的值为

A B．

B D．

正确答案

B

考查方向

本题主要考查了余弦定理的应用及三角函数的定义等知识，在近几年的各省高考题出现的频率较高，常以三角公式与正余定理等知识交汇命题，较易。

易错点

1、本题在把题意转化成余弦定理模型上易出错。

知识点

正弦定理余弦定理解三角形的实际应用

热门试卷

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

考查方向

易错点

知识点