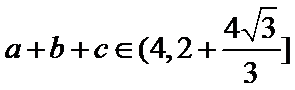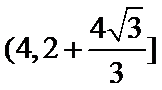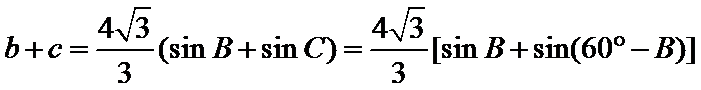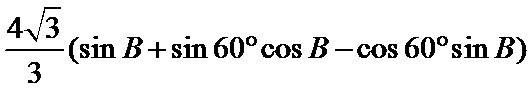- 正弦定理
- 共176题
9.在





正确答案
解析
在三角形中,利用三角形的内角和A+B+C= 

考查方向
解题思路
画出草图,标出已知信息,根据已知元素,合理准确地使用正、余弦定理求解。
易错点
根据已知额信息,不能如何准确地使用正、余弦定理求解。
知识点
16.已知向量
(I)求函数
(II)在




正确答案
(1)


(2)
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求
(Ⅰ)
=
由
所以函数的单调递增区间为[
(Ⅱ)
由
考查方向
解题思路
本题考查三角函数与解三角形,解题步骤如下:
1、利用向量的数量积求出
2、利用余弦定理求出
易错点
第一问中的辅助角容易计算错误
知识点
在△



17.若

18.若

正确答案

解析
试题分析:本题属于正余弦定理的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
因为



因为


因此
考查方向
解题思路
直接利用正弦定理及边角关系进行计算;
易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于正余弦定理的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
设



考查方向
解题思路
设


易错点
相关知识点不熟容易处错。
13.锐角三角形ABC中,


正确答案
解析
利用正弦定理得出
又∵
考查方向
解题思路
该题解题思路如下1、利用正弦定理得出


易错点
该题易于忽略了对A的范围的判断,该题属于中档题
知识点
已知



17.求
18.若

正确答案

解析
∵

∴




考查方向
解题思路
第一问中用两角和差公式和三角恒等变换化简得到

易错点
第一问中想不到将角

正确答案

解析
∵




∴


考查方向
解题思路
第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
第二问中用余弦定理求角时容易将特殊角记错。
在△ABC中,角A、B、C所对的边分别为a、b、c,且满足cos2C-cos2A=2sin(

17.求角A的值;
18.若a=
正确答案
见解析
解析
(1)由已知得
化简得


考查方向
解题思路
该题解题思路如下
1)利用倍角公式
2)利用特殊角的三角函数求值得到角A,
3)使用正弦定理,进行边角之间的转换
4)根据角的取值范围得到答案
易错点
该题易于忽略了对A的范围的判断,该题属于中档题
正确答案
见解析
解析
解:
(2)由正弦定理

故
因为


所以
考查方向
解题思路
该题解题思路如下
1)利用倍角公式
2)利用特殊角的三角函数求值得到角A,
3)使用正弦定理,进行边角之间的转换
4)根据角的取值范围得到答案
易错点
该题易于忽略了对A的范围的判断,该题属于中档题
在



17.求
18.若




正确答案
(1)
解析
试题分析:本题属于解三角形问题,属于基础题,主要考查两个定理的应用以及三角形的面积公式。具体解答步骤如下:
(Ⅰ)由正弦定理,
可得
所以
所以
因为


考查方向
解题思路
本题考查解三解形,解题步骤如下:
1)利用正弦定理及三角恒等变换求出C。
2)通过面积公式及
3)根据a,b的两组解分别求

易错点
1、利用余弦定理增加运算量; 2、第二问解三角形时遗漏一组解。
正确答案
(2)

解析
试题分析:本题属于解三角形问题,属于基础题,主要考查两个定理的应用以及三角形的面积公式。具体解答步骤如下:
(Ⅱ)解法一:由已知
所以


当

所以
所以


因为

在

当
所以

(Ⅱ)解法二:在


因为

由已知

又
解得
考查方向
解题思路
本题考查解三解形,解题步骤如下:
1)利用正弦定理及三角恒等变换求出C。
2)通过面积公式及
3)根据a,b的两组解分别求

易错点
1、利用余弦定理增加运算量; 2、第二问解三角形时遗漏一组解。
在△ABC中,已知a,b, c分别是角A,B,C的对边,且满足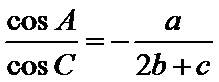
17.求角A的大小;
18.若a=2,求△ABC的周长的取值范围.
正确答案
(1)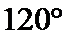
解析
(1)由正弦定理,得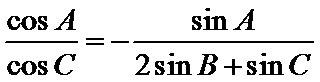
∴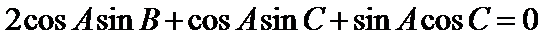
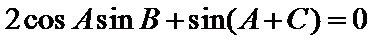
∵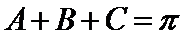
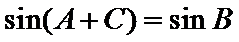
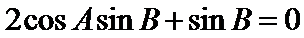
∵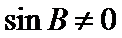
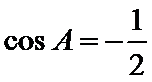
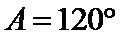
考查方向
解题思路
(1)利用已知条件和正弦定理求出角A(2)利用(1)中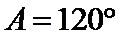
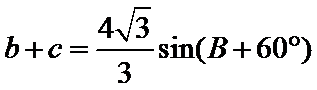
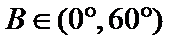
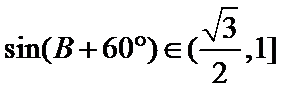
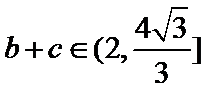
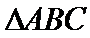
易错点
通过正弦定理表示三边即周长,易忽视角的范围出错。
正确答案
(2)
解析
(2)由正弦定理,得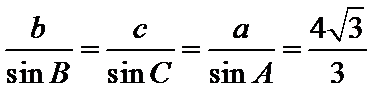
∴
=
=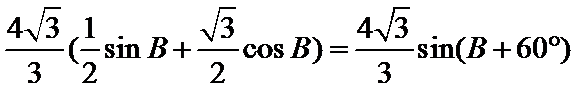
∵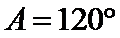
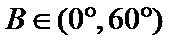
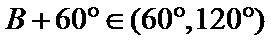
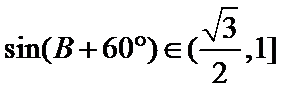
∴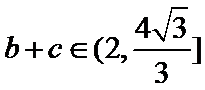
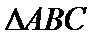
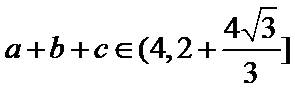
考查方向
解题思路
(1)利用已知条件和正弦定理求出角A(2)利用(1)中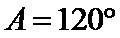
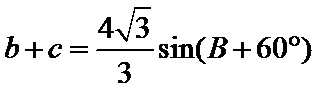
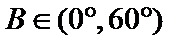
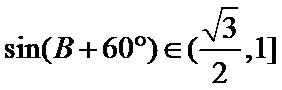
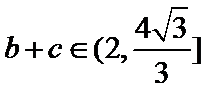
易错点
通过正弦定理表示三边即周长,易忽视角的范围出错。
5. 在




正确答案
解析
由正弦定理得



考查方向
解题思路
1.先利用正弦定理求出角C;2.利用大边对大角求出角C的准确值。
易错点
1.不知道应该用什么定理;2.不会根据大边对大角舍去一个角,导致结果出错。
知识点
6.在


正确答案
解析


考查方向
解题思路
根据所给条件,求出其他同角三角函数值
易错点
计算错误,忽略取值正负
知识点
扫码查看完整答案与解析