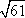· 解三角形

· 正弦定理

正弦定理
共176题

· 解三角形

· 正弦定理

正弦定理
共176题

热门试卷

X 查看更多试卷

1

题型：填空题

|

填空题 · 5 分

在中，若，，的面积为，则=（） .

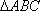
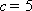
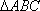
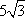
正确答案

解析

略

知识点

正弦定理

1

题型：填空题

|

填空题 · 5 分

在△中，，，，则的值为　　　　。

正确答案

解析

略

知识点

正弦定理

1

题型：简答题

|

简答题 · 13 分

在中，分别为角的对边，且满足。

（1）求角的值；

（2）若，设角的大小为，的周长为，求的最大值。

正确答案

（1）

解析

（1）∵，

∴

又，

∴； -------------------5分

（2）∵，

∴

同理

∴

∵∴，

∴即时，.-------------------13分

知识点

正弦定理余弦定理三角函数的最值

1

题型：简答题

|

简答题 · 12 分

如图，在△ABC中，∠C=45°，D为BC中点，BC=2.记锐角∠ADB=α，且满足cos2α=。

（1）求cosα；

（2）求BC边上高的值。

正确答案

见解析。

解析

（1）∵cos2α=2cos2α﹣1=，

∴，

∵，

∴cosα=，

（2）方法一、由（1）得=，

∵∠CAD=∠ADB﹣∠C=α﹣45°，

∴sin∠CAD=sin（）=sin

==，

在△ACD中，由正弦定理得：，

∴AD==，

则高h=ADsin∠ADB==4。

方法二、如图，作BC 边上的高为AH

在直角△△ADH中，由（1）可得=，

则不妨设AD=5m则DH=3m，AH=4m﹣

注意到C=45°，则△AHC为等腰直角三角形，所以CD+DH=AH，

则1+3m=4m﹣

所以m=1，即AH=4

知识点

二倍角的余弦正弦定理

1

题型：简答题

|

简答题 · 14 分

如图所示，扇形，圆心角的大小等于，半径为，在半径上有一动点，

过点作平行于的直线交弧于点。

（1）若是半径的中点，求线段的大小；

（2）设，求△面积的最大值及此时的值。

正确答案

（1）（2）

解析

解析：

（1）在△中，，

由

得，解得。

（2）∵∥，∴，

在△中，由正弦定理得，即

∴,又。

解法一：记△的面积为，则，

∴时，取得最大值为.

解法二：

即，又即

当且仅当时等号成立,

所以

∴时，取得最大值为.

知识点

两角和与差的余弦函数正弦定理

继续学习学习下一知识点

下一知识点 : 正弦定理的应用

百度题库 > 高考 > 理科数学 > 正弦定理

扫码查看完整答案与解析