- 解三角形的实际应用
- 共67题
已知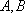

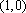
(1)当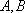

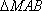
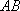
(2)当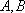

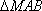
正确答案
见解析
解析
(1) 设
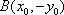
因为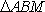
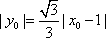
又点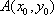
所以 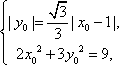
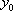
得到 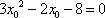
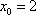
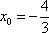
当

当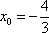
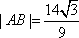
{说明:若少一种情况扣2分}
(2)法1:根据题意可知,直线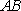
设直线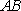
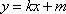
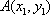
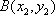
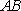
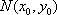
联立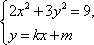


由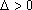
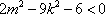
所以
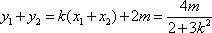
所以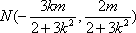
如果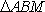
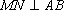
所以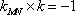
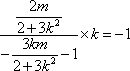
化简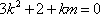
由②得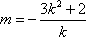
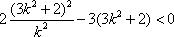
化简得 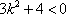
{此步化简成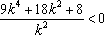
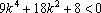

故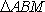
法2:设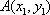
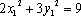
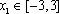
所以 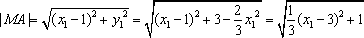
设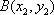
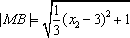
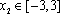
因为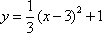

所以,有
因为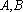

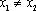
所以
所以
知识点
在










(1)求边
(2)求
正确答案
(1)
(2)
解析
(1)由

所以
由

所以
(2)由

所以
所以
知识点
如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登,已知



正确答案
能
解析
由

由正弦定理得

在

即

解得

由于
知识点
北京2008年第29届奥运会开幕式上举行升旗仪式,在坡度
15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的
仰角分别为60°和30°,第一排和最后一排的距离为
(如图所示),则旗杆的高度为
正确答案
解析
略
知识点
已知条件

① 


③ 


则其中是
正确答案
①③④
解析
略
知识点
某人沿一条折线段组成的小路前进,从










试画出大致示意图,并计算出从

正确答案
见解析
解析
示意图,如图所示,
连接AC,在△ABC中,∠ABC=50°+(180°-110°)=120°,
又AB=BC=3,∴∠BAC=∠BCA=30°
由余弦定理可得
在△ACD中,∠ACD=360°-140°-(70°+30°)=120°,CD=3
由余弦定理得AD=
=

由正弦定理得sin∠CAD=
∴∠CAD=45°,于是AD的方位角为50°+30°+45°=125°,
所以,从A到D的方位角是125°,距离为
知识点
如图2,一条河的两岸平行,河的宽度
一艘客船从码头

已知

驶完航程所用最短时间为
的速度大小为
正确答案
解析
略
知识点
已知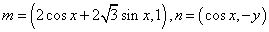
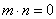
(1)将y表示为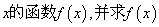
(2)已知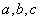
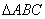

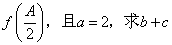
正确答案
见解析。
解析
知识点
已知函数

(1)求函数
(2)已知







正确答案
见解析。
解析
(1)



由





(2)∵


∵


即

由余弦定理

即

∴
知识点
已知抛物线型拱桥的顶点距水面



正确答案
5.66
解析
略
知识点
扫码查看完整答案与解析