- 解三角形的实际应用
- 共67题
已知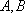

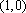
(1)当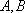

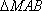
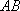
(2)当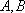

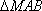
正确答案
见解析
解析
(1) 设
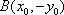
因为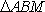
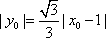
又点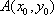
所以 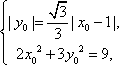
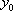
得到 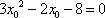
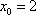
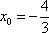
当

当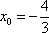
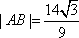
{说明:若少一种情况扣2分}
(2)法1:根据题意可知,直线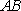
设直线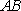
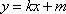
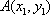
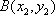
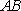
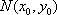
联立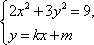


由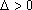
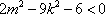
所以
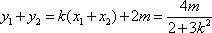
所以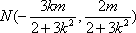
如果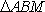
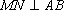
所以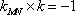
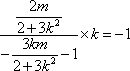
化简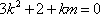
由②得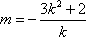
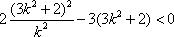
化简得 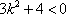
{此步化简成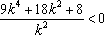
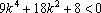

故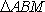
法2:设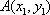
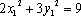
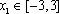
所以 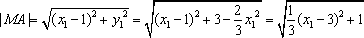
设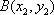
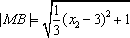
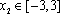
因为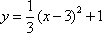

所以,有
因为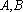

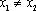
所以
所以
知识点
在










(1)求边
(2)求
正确答案
(1)
(2)
解析
(1)由

所以
由

所以
(2)由

所以
所以
知识点
已知条件

① 


③ 


则其中是
正确答案
①③④
解析
略
知识点
已知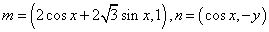
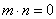
(1)将y表示为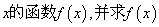
(2)已知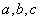
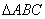

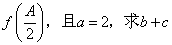
正确答案
见解析。
解析
知识点
已知函数

(1)求函数
(2)已知







正确答案
见解析。
解析
(1)



由





(2)∵


∵


即

由余弦定理

即

∴
知识点
扫码查看完整答案与解析