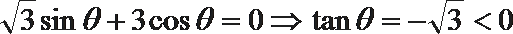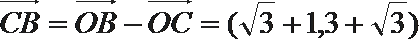- 解三角形的实际应用
- 共67题
19.在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域,点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船位于点A北偏东45º且与点A相距40




(1)求该船的行驶速度(单位:海里/小时)
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,海上有






(1)用



(2)晚上小艇在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18 .已知函数
(1)求函数
(2)已知






正确答案
(1)原式整理得
对称中心为
单调减区间为
(2)∵

∴C=
∵

及由正弦定理得
由余弦定理得
∴
解析
解析已在路上飞奔,马上就到!
知识点
17. 如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?
正确答案
在△BDC中,由余弦定理知cos∠CDB=
sin∠CDB=
∴轮船距港口A还有15海里.
解析
解析已在路上飞奔,马上就到!
知识点
21. 如下图,某小区准备绿化一块直径为










(1)试用



(2)若

正确答案
(1)在

设正方形的边长为

由

所以
(2)
令


所以

所以函数

因此当


所以当
解析
解析已在路上飞奔,马上就到!
知识点
6.如图,




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量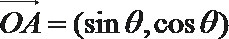
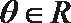
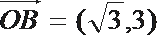
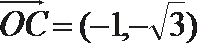
(1)若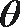
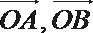
(2)若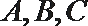
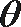
正确答案
解:(1)假设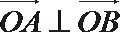
即
而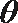
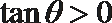
即若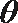
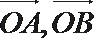
(2)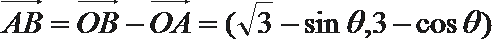
由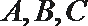
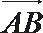
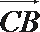
所以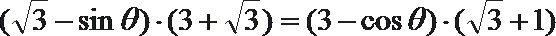
化简得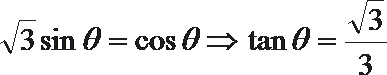
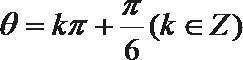
解析
解析已在路上飞奔,马上就到!
知识点
4.某观察站









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,某观测站C在城A的南偏西

正确答案
解:在


所以
在

所以
由正弦定理

故这时此车距离A城15千米
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析