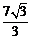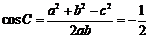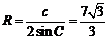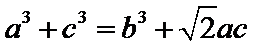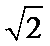- 解三角形的实际应用
- 共67题
9. 已知
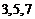
正确答案
解析
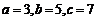
∴
∴
知识点
如图,












22. 求

23. 已知警员的对讲机的有效通话距离是3千米.当



正确答案
(1)

解析
试题分析: (1)由题意可得

(1)


所以

考查方向
解题思路
解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.
易错点
实际问题数学模型的转化
正确答案
(2)超过了3千米.
解析
试题分析: (2) 分段求出对应函数解析式,根据函数单调性求得最值即可.
(2)当



所以

所以

当


所以
所以
所以当 


考查方向
解题思路
解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.
易错点
分段函数单调性最值的求解
15. 在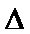
(I)求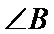
(II)求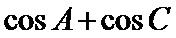
正确答案
知识点


17.求角B的大小;
18.若BD为AC边上的中线,

正确答案
见解析
解析









考查方向
解题思路
利用正弦定理求角度
易错点
正弦定理、余弦定理的性质掌握不好
正确答案
见解析
解析
法一:在三角形









法二: 延长













考查方向
解题思路
用余弦定理求面积
易错点
正弦定理、余弦定理的性质掌握不好
15. 在

(1)求
(2)若点D在


正确答案
见解析
解析
解:如图, 设




又由正弦定理得
由题设知

在

考查方向
解题思路
(1)用余弦定理求a
(2)由正弦定理求sinB
(3)在
易错点
忽略数形结合思想在本题中的作用。
知识点
扫码查看完整答案与解析