- 弧度制的应用
- 共31题
已知a,b,m,n均为正数,且a+b=1,mn=2,则(am+bn)(bm+an)的最小值为__________。
正确答案
2
解析
(am+bn)(bm+an)=abm2+(a2+b2)mn+abn2=ab(m2+n2)+2(a2+b2)≥2abmn+2(a2+b2)=4ab+2(a2+b2)=2(a2+2ab+b2)=2(a+b)2=2(当且仅当m=n=
知识点
设数列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,

(1)求集合P11中元素的个数;
(2)求集合P2 000中元素的个数。
正确答案
(1)5; (2) 1 008
解析
解:(1)由数列{an}的定义得a1=1,a2=-2,a3=-2,a4=3,a5=3,a6=3,a7=-4,a8=-4,a9=-4,a10=-4,a11=5,所以S1=1,S2=-1,S3=-3,S4=0,S5=3,S6=6,S7=2,S8=-2,S9=-6,S10=-10,S11=-5,从而S1=a1,S4=0×a4,S5=a5,S6=2a6,S11=-a11,所以集合P11中元素的个数为5.
(2)先证:Si(2i+1)=-i(2i+1)(i∈N*)。
事实上,①当i=1时,Si(2i+1)=S3=-3,-i(2i+1)=-3,故原等式成立;
②假设i=m时成立,即Sm(2m+1)=-m(2m+1),则i=m+1时,S(m+1)(2m+3)=Sm(2m+1)+(2m+1)2-(2m+2)2=-m(2m+1)-4m-3=-(2m2+5m+3)=-(m+1)(2m+3)。
综合①②可得Si(2i+1)=-i(2i+1),于是S(i+1)(2i+1)=Si(2i+1)+(2i+1)2=-i(2i+1)+(2i+1)2=(2i+1)(i+1)。
由上可知Si(2i+1)是2i+1的倍数,而ai(2i+1)+j=2i+1(j=1,2,…,2i+1),所以Si(2i+1)+j=Si(2i+1)+j(2i+1)是ai(2i+1)+j(j=1,2,…,2i+1)的倍数,又S(i+1)(2i+1)=(i+1)(2i+1)不是2i+2的倍数,而a(i+1)(2i+1)+j=-(2i+2)(j=1,2,…,2i+2),所以S(i+1)(2i+1)+j=S(i+1)(2i+1)-j(2i+2)=(2i+1)(i+1)-j(2i+2)不是a(i+1)(2i+1)+j(j=1,2,…,2i+2)的倍数,故当l=i(2i+1)时,集合Pl中元素的个数为1+3+…+(2i-1)=i2,于是,当l=i(2i+1)+j(1≤j≤2i+1)时,集合Pl中元素的个数为i2+j.
又2 000=31×(2×31+1)+47,故集合P2 000中元素的个数为312+47=1 008.
知识点
函数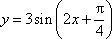
正确答案
π
解析
函数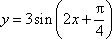
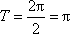
知识点
如图,AB和BC分别与圆O相切于点D,C,AC经过圆心O,且BC=2OC.
正确答案
见解析
解析
证明:连结OD.因为AB和BC分别与圆O相切于点D,C,
所以∠ADO=∠ACB=90°。
又因为∠A=∠A,所以Rt△ADO∽Rt△ACB.
所以
又BC=2OC=2OD,故AC=2AD.
知识点
设变量x,y满足约束条件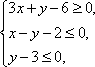
正确答案
解析
作约束条件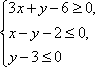
知识点
扫码查看完整答案与解析


