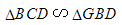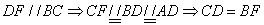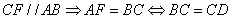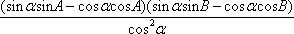- 弧度制的应用
- 共31题
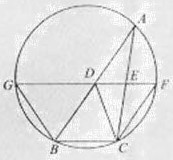
如图,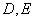
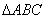
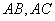
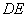
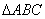
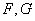
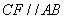
证明:
(1)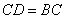
(2)
正确答案
见解析
解析
(1)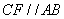
(2)
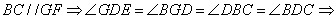
知识点
若
正确答案
解析
设
所以

同理

知识点
在△ABC中,内角A,B,C的对边分别是a,b,c,且a2+b2+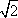
(1)求C;
(2)设cos Acos B=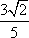
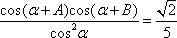
正确答案
(1) 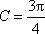
解析
(1)因为a2+b2+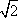
由余弦定理有cos C=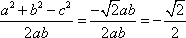
故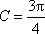
(2)由题意得
=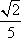
因此(tan αsin A-cos A)(tan αsin B-cos B)=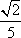
tan2αsin Asin B-tan α(sin Acos B+cos Asin B)+cos Acos B=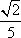
tan2αsin Asin B-tan αsin(A+B)+cos Acos B=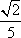
因为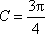
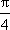
所以sin(A+B)=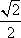
因为cos(A+B)=cos Acos B-sin Asin B,
即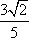
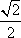
解得sin Asin B=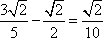
由①得tan2α-5tan α+4=0,
解得tan α=1或tan α=4
知识点
某几何体的三视图如图所示,则其体积为__________。
正确答案
解析
由三视图可知该几何体是如图所示的半个圆锥,底面半圆的半径r=1,高SO=2,则V几何体=
知识点
设a,b为向量,则“|a·b|=|a||b|”是“a∥b”的( )。
正确答案
解析
若a与b中有一个为零向量,则“|a·b|=|a||b|”是“a∥b”的充分必要条件;若a与b都不为零向量,设a与b的夹角为θ,则a·b=|a||b|cos θ,由|a·b|=|a||b|得|cos θ|=1,则两向量的夹角为0或π,所以a∥b.若a∥b,则a与b同向或反向,故两向量的夹角为0或π,则|cos θ|=1,所以|a·b|=|a||b|,故“|a·b|=|a||b|”是“a∥b”的充分必要条件
知识点
扫码查看完整答案与解析